某“帆板”集训队在一海滨区域进行集训，该海滨区域的海浪高度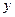
（米）随着时间
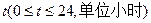而周期性变化，每天各时刻
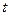的浪高数据的平均值如下表：
 |
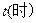0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
 |
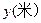1．0 |
1．4 |
1．0 |
0．6 |
1．0 |
1．4 |
0．9 |
0．5 |
1．0 |
（Ⅰ）试画出散点图；
（Ⅱ）观察散点图，从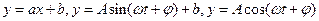
中选择一个合适的函数模型，并求出该拟合模型的解析式；
（Ⅲ）如果确定在白天7时~19时当浪高不低于0。8米时才进行训练，试安排恰当的训练时间。
，求证：
.
取什么数值时，复数
分别是：
在
处取得极值，且曲线
在点
处的切线垂直于直线
.
的值；
，若方程
有三个不相等的实根，求
的取值范围.
的单调性；
时，求函数
上的最值.
是
的极值点，求
上的单调递增函数，求实数
的取值范围.