定义在区间(0, )上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有
)上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有 .
.
(1)求证:方程f(x)=0有且只有一个实根;
(2)若a>b>c>1,且a、b、c成等差数列,求证: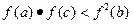 ;
;
(3)(本小题只理科做)若f(x) 单调递增,且m>n>0时,有 ,求证:
,求证: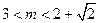
(本小题12分)已知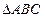 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、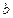 、
、 ,且
,且 。
。
(I)求 的值;
的值;
(II)若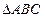 的面积
的面积 ,且
,且 ,求
,求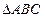 的外接圆半径
的外接圆半径 。
。
(本小题满分12分)选修4-1:几何证明选讲.
如图所示,已知 与⊙
与⊙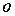 相切,
相切, 为切点,
为切点,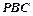 为割线,
为割线,
弦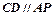 ,
, 相交于
相交于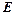 点,
点,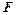 为
为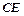 上一点,
上一点,
且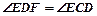 .
.
(1)求证: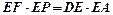 ;
;
(2)若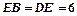 ,
, ,求
,求 的长.
的长.
(本小题满分12分)
已知函数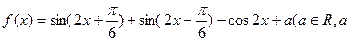 为常数).
为常数).
(1)求函数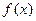 的最小正周期;(2)求函数
的最小正周期;(2)求函数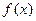 的单调递增区间;
的单调递增区间;
(3) 若 时,
时,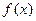 的最小值为
的最小值为 ,求
,求 的值.
的值.
(本小题满分10分)选修4-5:不等式选讲
(I)已知 都是正实数,求证:
都是正实数,求证: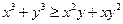 ;
;
(II)设函数 ,解不等式
,解不等式 .
.
已知A、B是圆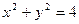 上满足条件
上满足条件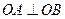 的两个点,其中O是坐标原点,
的两个点,其中O是坐标原点, 分别过A、B作
分别过A、B作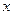 轴的垂线段,交椭圆
轴的垂线段,交椭圆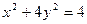 于
于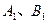 点,动点P满足
点,动点P满足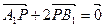 .(1)求动点P的轨迹方程;(2)设S1和S2
.(1)求动点P的轨迹方程;(2)设S1和S2 分别表示
分别表示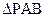 和
和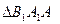 的面积,当点P在x轴的上方,点A在x轴的下方时,求
的面积,当点P在x轴的上方,点A在x轴的下方时,求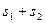 的最大值。
的最大值。