在平面直角坐标系内有两个定点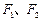 和动点P,
和动点P,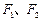 坐标分别为
坐标分别为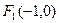 、
、 ,动点
,动点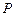 满足
满足 ,动点
,动点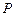 的轨迹为曲线
的轨迹为曲线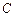 ,曲线
,曲线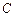 关于直线
关于直线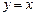 的对称曲线为曲线
的对称曲线为曲线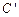 ,直线
,直线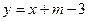 与曲线
与曲线 交于A、B两点,O是坐标原点,△ABO的面积为
交于A、B两点,O是坐标原点,△ABO的面积为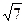 ,
,
(1)求曲线C的方程;(2)求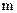 的值。
的值。
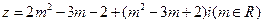 在复平面内对应的点在第三象限。
在复平面内对应的点在第三象限。
⑴求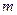 的取值范围;
的取值范围;
⑵求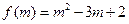 的最小值,并求出此时
的最小值,并求出此时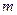 的值。
的值。
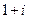 是关于
是关于 的方程
的方程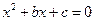 的一个根
的一个根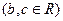
⑴求 的值;
的值;
⑵试说明 也是方程的一个根。
也是方程的一个根。
设数列{ }的前
}的前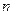 项和为
项和为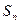 ,且方程
,且方程 有一根为
有一根为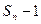 ,
,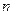 =1,2,3,….
=1,2,3,….
(1)求 ;
;
(2)猜想数列{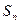 }的通项公式,并给出严格的证明.
}的通项公式,并给出严格的证明.
某种产品的广告费支出 与销售额(单位:百万元)之间有如下对应数据:
与销售额(单位:百万元)之间有如下对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
50 |
60 |
70 |
如果 与
与 之间具有线性相关关系.
之间具有线性相关关系.
(1)作出这些数据的散点图;(2)求这些数据的线性回归方程;
(3)预测当广告费支出为9百万元时的销售额.
设函数 ,曲线
,曲线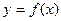 在点(
在点( ,
,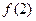 )处的切线方程为
)处的切线方程为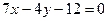 .
.
(1)求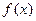 的解析式;
的解析式;
(2)证明:曲线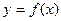 任一点处的切线与直线
任一点处的切线与直线 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.