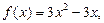
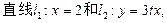

 。直线l2与函数
。直线l2与函数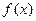 的图象以及直线l1、l2与函数
的图象以及直线l1、l2与函数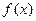 的图象
的图象
围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为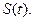
(1)求函数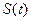 的解析式;
的解析式;
(2)若函数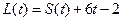 ,判断
,判断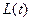 是否存在极值,若存在,求出极值,若不存在,说明理由;
是否存在极值,若存在,求出极值,若不存在,说明理由;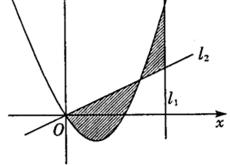
求经过直线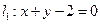 与直线
与直线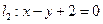 的交点且平行于直线
的交点且平行于直线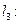
 的直线
的直线 的方程.
的方程.
某厂根据市场需求开发折叠式小凳(如图所示). 凳面为三角形的尼龙布,凳脚为三根细钢管. 考虑到钢管的受力和人的舒适度等因素,设计小凳应满足:① 凳子高度为 ,② 三根细钢管相交处的节点
,② 三根细钢管相交处的节点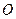 与凳面三角形
与凳面三角形 重心的连线垂直于凳面和地面. (1)若凳面是边长为
重心的连线垂直于凳面和地面. (1)若凳面是边长为 的正三角形,三只凳脚与地面所成的角均为
的正三角形,三只凳脚与地面所成的角均为 ,确定节点
,确定节点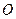 分细钢管上下两段的比值;
分细钢管上下两段的比值;
(2)若凳面是顶角为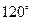 的等腰三角形,腰长为
的等腰三角形,腰长为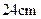 ,节点
,节点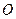 分细钢管上下两段之比为
分细钢管上下两段之比为 . 确定三根细钢管的长度.
. 确定三根细钢管的长度.
(本小题满分12分) 甲、乙两人在一场五局三胜制的象棋比赛中,规定甲或乙无论谁先赢满三局就获胜,并且比赛就此结束.现已知甲、乙两人每比赛一局甲取胜的概率是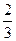 ,乙取胜的概率为
,乙取胜的概率为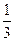 ,且每局比赛的胜负是独立的,试求下列问题:
,且每局比赛的胜负是独立的,试求下列问题:
(Ⅰ)比赛以甲3胜1而结束的概率;
(Ⅱ)比赛以乙3胜2而结束的概率;
(Ⅲ)设甲获胜的概率为a,乙获胜的概率为b,求a:b的值.
(本小题满分12分)如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,
AB=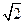 ,AF=1,M是线段EF的中点。
,AF=1,M是线段EF的中点。
(Ⅰ)求证:AM∥平面BDE;
(Ⅱ) 求二面角A-DF-B的大小.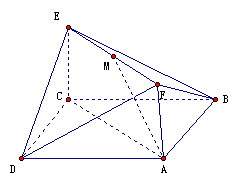
(本小题满分12分)学习小组有6个同学,其中4个同学从来没有参加过数学研究性学习活动,2个同学曾经参加过数学研究性学习活动.
(1)现从该小组中任选2个同学参加数学研究性学习活动,求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;
(2)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,求该小组没有参加过数学研究性学习活动的同学个数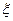 取2,3,4时的概率
取2,3,4时的概率