已知函数y=f(x)是定义在区间[-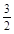 ,
,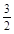 ]上的偶函数,且
]上的偶函数,且
x∈[0,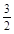 ]时,
]时,
(1)求函数f(x)的解析式;
(2)若矩形ABCD的顶点A,B在函数y=f(x)的图像上,顶点C,D在x轴上,求矩形ABCD面积的最大值.
等比数列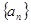 中,
中,  ,
, ,求
,求 .
.
在△ABC中,已知 ,
,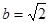 ,B=45°求A、C及c
,B=45°求A、C及c
椭圆
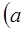 >
> >
>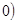 与直线
与直线 交于
交于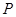 、
、 两点,且
两点,且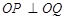 ,其中
,其中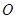 为坐标原点.
为坐标原点.
(1)求 的值;
的值;
(2)若椭圆的离心率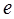 满足
满足 ≤
≤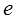 ≤
≤ ,求椭圆长轴的取值范围.
,求椭圆长轴的取值范围.
某校高三数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示.若130~140分数段的人数为2人.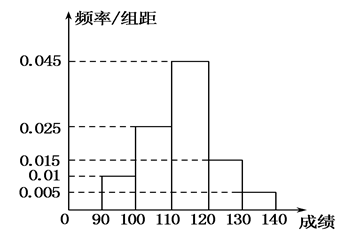
(1)求这组数据的平均数M;
(2)现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成帮扶学习小组.若选出的两人成绩之差大于20,则称这两人为“黄金搭档组”,试求选出的两人为“黄金搭档组”的概率.
椭圆 的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,,|PF1|=
的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,,|PF1|=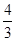 ,
,
|PF2|= .
.
(1)求椭圆C的方程;
(2)若直线L过圆(x+2)2+(y-1)2=5的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程。