 某售货员负责在甲、乙、丙三个柜面上售货.如果在某一小时内各柜面不需要售货员照顾的概率分别为0.9,0.8,0.7.假定各个柜面是否需要照顾相互之间没有影响,求在这个小时内:
某售货员负责在甲、乙、丙三个柜面上售货.如果在某一小时内各柜面不需要售货员照顾的概率分别为0.9,0.8,0.7.假定各个柜面是否需要照顾相互之间没有影响,求在这个小时内:
(1)只有丙柜面需要售货员照顾的概率;
(2)三个柜面最多有一个需要售货员照顾的概率;
(3)三个柜面至少有一个需要售货员照顾的概率.
(本小题满分10分)
已知点A(-3,-4)、B(5,-12)
(1)求 的坐标及|
的坐标及| |;
|;
(2)若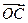 =
=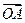 +
+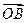 ,
,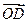 =
=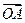 -
-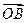 ,求
,求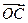 及
及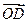 的坐标;
的坐标;
(3)求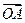 ·
·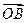

(本小题满分14分)
如图半圆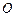 的直径为2,
的直径为2,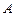 点在直径的延长线上,且
点在直径的延长线上,且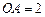 ,
,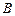 点为半圆周上的任意一点,以
点为半圆周上的任意一点,以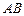 为边作一个等边
为边作一个等边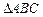 ,问
,问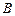 点在什么位置时,四边形
点在什么位置时,四边形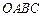 的面积最大?并求出此时的四边形面积.
的面积最大?并求出此时的四边形面积.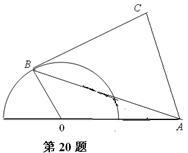

(本小题满分14分)
已知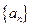 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,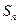 为
为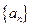 的前
的前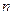 项和.
项和.
(1)求通项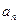 及
及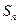 ;
;
(2)设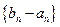 是首项为1,公比为3的等
是首项为1,公比为3的等 比数列,求数列
比数列,求数列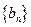 的通项公式及其前
的通项公式及其前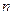 项和
项和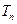 .
.
(本题满分12分)
某文具店购进一批新型台灯,若按每盏台灯15元的价格销售. 每天能卖出30盏,若售价每提高1元,日销售量将减少2盏.
(1)设这批台灯提价后每盏的销售价格定为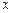 ,销售收入为
,销售收入为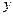 ,写出
,写出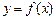 .
.
(2)为了使这批台灯每天获得400元以上的销售收入,问应如何制定这批台灯每盏的销售价格范围?
(本题满分14分)
关于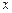 的不等式
的不等式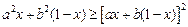
(1)当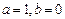 时解不等式;
时解不等式;
(2)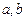
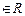 ,
,  解不等式.
解不等式.