某小区要建一座八边形的休闲小区,它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200 m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如ΔDQH等)上铺草坪,造价为80元/m2。
设总造价为S元,AD长为xm,试建立S与x的函数关系;
当x为何值时,S最小?并求这个最小值。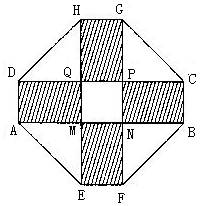
如图,在直三棱柱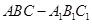 中,
中,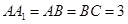 ,
,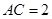 ,
, 是
是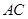 的中点.
的中点.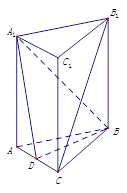
(Ⅰ)求证:  平面
平面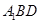 ;
;
(Ⅱ)求二面角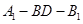 的余弦值.
的余弦值.
一个盒子中装有分别标有数字1、2、3、4的4个大小、形状完全相同的小球,现从中有放回地随机抽取2个小球,抽取的球的编号分别记为 、
、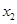 ,记
,记 .
.
(Ⅰ)求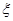 取最大值的概率;
取最大值的概率;
(Ⅱ)求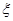 的分布列及数学期望.
的分布列及数学期望.
已知抛物线 ,点P(-1,0)是其准线与
,点P(-1,0)是其准线与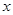 轴的焦点,过P的直线
轴的焦点,过P的直线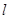 与抛物线C交于A、B两点.
与抛物线C交于A、B两点.
(1)当线段AB的中点在直线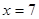 上时,求直线
上时,求直线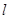 的方程;
的方程;
(2)设F为抛物线C的焦点,当A为线段PB中点时,求△FAB的面积.
四棱锥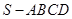 中,底面
中,底面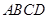 为平行四边形,侧面
为平行四边形,侧面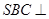 底面
底面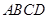 .已知
.已知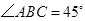 ,
,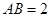 ,
,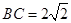 ,
,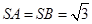 .
.
(Ⅰ)证明 ;
;
(Ⅱ)求直线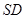 与平面
与平面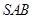 所成角的正弦值.
所成角的正弦值.
已知函数
(Ⅰ)若 ,求
,求 的极大值;
的极大值;
(Ⅱ)若 在定义域内单调递减,求满足此条件的实数k的取值范围.
在定义域内单调递减,求满足此条件的实数k的取值范围.