质量m=10×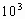
kg的汽车，在平直路面上行驶时，其发动机的功率和所受阻力不变，已知汽车速度为
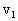=5m／s时，其加速度为
=0.75
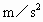；汽车速度为
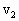=10m／s时，加速度为
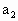=0.25
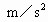．试求：
(1)汽车发动机的功率P；
(2)汽车可能达到的最大速度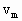
．
一个质量为m的带正电荷的小球，栓在一根长为L的绝缘轻绳上，绳的另一个端固定在O点，小球位于水平向右的匀强电场中，平衡时细绳与竖直方向成α角，如图所示，现在用力使小球移到O点的竖直下方，绳被拉直，从静止释放小球，求它回到平衡位置时绳的拉力多大?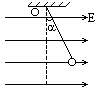
在真空管内，阴极与阳极之间的电压为36V，阴极加热后发射热电子打在阳极上，测得阳极电流 I 为3.2mA．计算：(1)阴极每秒钟发射出的电子数；(2)假设电子离开阴极的速度为零，电子达到阳极前的速度是多大?(3)阳极上受到的撞击力大小?(4)阳极上由于电子碰撞，每秒钟产生的热量是多少焦（电子质量m=0.91×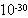
kg）？
如图所示，一个倾角为θ的绝缘斜面固定在场强为E的匀强电场中．有一个质量为m、电荷量为正q的物体以初速度V0从斜面底端A沿斜面向上运动至B，接着又沿斜面向下运动返回A点，此时速度为V，若AB长为L，求物体与斜面间动摩擦因数μ．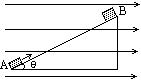
如图所示，质量为m，带电量为q的小球以初速v0从斜面上水平抛出，并落在斜面上．已知斜面倾角为θ，重力加速度为g，空间存在着方向水平向右的匀强电场，场强大小为E．求小球运动过程中离斜面的最远距离以及离出发点的最远距离各是多少？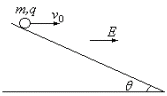
测定电子荷质比e/m的精确的现代方法之一是双电容器法，装置如图所示．在真空管中由阴极K发射出电子，其初速度可以忽略不计．此电子被阴极K与阳极A间的电场加速后穿过屏障D1上的小孔，然后顺序穿过电容器C1、屏障D2上的小孔和第二个电容器C2而射到荧光屏F上．阳极与阴极间的电势差为U．在电容器C1、C2之间加有频率为f的完全相同的交流电压，C1、C2之间的距离为l．选择频率f使电子束在荧光屏上的亮点不发生偏转，试证明电子的荷质比为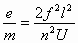
．其中n为奇数．