已知函数f(x)＝x3＋bx2＋ax＋d的图象过点P（0，2），且在点M（－1，f（－1））处的切线方程为6x-y+7=0.（Ⅰ）求函数y=f(x)的解析式；（Ⅱ）求函数y=f(x)的单调区间.
(12分)
已知a、b、c是互不相等的非零实数.
求证：三个方程ax2+2bx+c=0，bx2+2cx+a=0，cx2+2ax+b=0至少有一个方程有两个相异实根.
设复数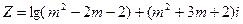
，试求实数m取何值时
（1）Z是实数；
（2）Z是纯虚数；
（3）Z对应的点位于复平面的第一象限
（本小题满分10分）
设函数
．
（I）若当
时，不等式
恒成立，求实数m的取值范围；
（II）若关于x的方程
在区间[0，2]上恰好有两个相异的实根，求实数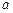
的取值范围．
（本小题满分10分）
（I）
两数的最大公约数为400，则两数的公约数的个数是；
（II）某人有4种颜色的灯泡（每种颜色的灯泡足够多），要在如图所示的6个点A、B、C、
上各装一个灯泡.要求同一条线段两端的灯泡不同色，则每种颜色的灯泡都至少用
一个的安装方法共有种（用数字作答）．
（本小题满分1
0分）
已知函数
．
（I）求
的单调区间；
（II）设
，若对任意
，均存在
，使得
，求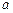
的取值范围．