(本小题满分10分)
(I) 两数的最大公约数为400,则两数的公约数的个数是 ;
两数的最大公约数为400,则两数的公约数的个数是 ;
(II)某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图所示的6个点A、B、C、 上各装一个灯泡.要求同一条线段两端的灯泡不同色,则每种颜色的灯泡都至少用
上各装一个灯泡.要求同一条线段两端的灯泡不同色,则每种颜色的灯泡都至少用 一个的安装方法共有 种(用数字作答).
一个的安装方法共有 种(用数字作答).
(本小题满分12分)已知命题 ,命题
,命题 的定义域为R,若
的定义域为R,若 ,求实数
,求实数 的取值范围。
的取值范围。
点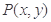 为曲线
为曲线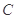 上任一点,点
上任一点,点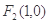 ,直线
,直线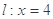 ,点
,点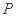 到直线
到直线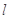 的距离为
的距离为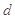 ,且满足
,且满足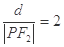 .
.
(1)求曲线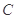 的轨迹方程;
的轨迹方程;
(2)点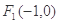 ,点
,点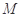 为直线
为直线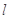 上的一个动点,且直线
上的一个动点,且直线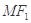 与曲线
与曲线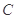 交于两点
交于两点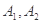 ,直线
,直线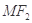 与曲线
与曲线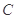 交于两点
交于两点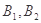 ,求
,求 的取值范围.
的取值范围.
已知椭圆C:
 过点
过点 ,且离心率为
,且离心率为 .
.
(1)求椭圆的标准方程;
(2)过右焦点的直线 与椭圆
与椭圆 相交于
相交于 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程.
已知 为椭圆C:
为椭圆C:
 的左右焦点,椭圆上的点到
的左右焦点,椭圆上的点到 的最近距离为2,且离心率为
的最近距离为2,且离心率为 .
.
(1)椭圆C的方程;
(2)若 是椭圆C上的动点,求
是椭圆C上的动点,求 的最大值和最小值.
的最大值和最小值.
已知椭圆C: 的两焦点为
的两焦点为 ,长轴两顶点为
,长轴两顶点为 .
.
(1) 是椭圆上一点,且
是椭圆上一点,且 ,求
,求 的面积;
的面积;
(2)过椭圆的左焦点作一条倾斜角为45°的直线 与椭圆交于
与椭圆交于 两点,求弦长
两点,求弦长 .
.