(本小题满分12分)
设函数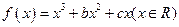 ,已知
,已知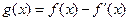 是奇函数。
是奇函数。
(1)求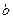 、
、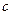 的值。
的值。
(2)求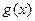 的单调区间与极值。
的单调区间与极值。
已知x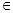 [-3,2],求f(x)=
[-3,2],求f(x)= 的最小值与最大值。
的最小值与最大值。

(本小题满分10分)
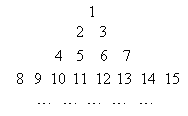
把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第 行共有
行共有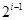 个正整数,设
个正整数,设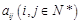 表示位于这个数表中从上往下数第
表示位于这个数表中从上往下数第 行,从左往右第
行,从左往右第 个数.
个数.
(1)求 的值;
的值;
(2)用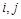 表示
表示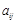 ;
;
(3)记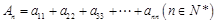 ,求证:当
,求证:当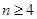 时,
时,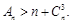
(本小题满分10分)
在平面直角坐标系xOy中,已知点 ,P是动点,且三角形POA的三边所在直线的斜
,P是动点,且三角形POA的三边所在直线的斜
率满足kOP+kOA=kPA.
(1)求点P的轨迹C的方程;
(2)若Q是轨迹C上异于点P的一个点,且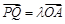 ,直线OP与QA交于点M,问:是否存在点P使得△PQA和△PAM的面积满足
,直线OP与QA交于点M,问:是否存在点P使得△PQA和△PAM的面积满足 ?若存在,求出点P的坐标;若不存在,说明理由.
?若存在,求出点P的坐标;若不存在,说明理由.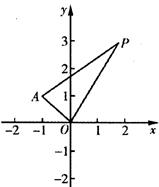
B选修4-4:坐标系与参数方程(本小题满分10分)
在直角坐标系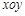 中,直线
中,直线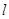 的参数方程为
的参数方程为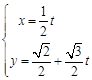 (
(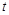 为参数),若以直角坐标系
为参数),若以直角坐标系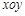 的
的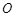 点为极点,
点为极点, 为极轴,且长度单位相同,建立极坐标系,得曲线
为极轴,且长度单位相同,建立极坐标系,得曲线 的极坐标方程为
的极坐标方程为 .
.
(1)求直线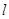 的倾斜角;
的倾斜角;
(2)若直线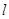 与曲线
与曲线 交于
交于 两点,求
两点,求 .
.