给出定义在(0，＋∞)上的三个函数：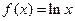
，
，
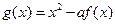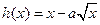，已知
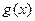在x＝1处取极值.
（Ⅰ）确定函数h(x)的单调性；
（Ⅱ）求证：当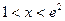
时，恒有
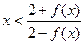成立；
（Ⅲ）把函数h(x)的图象向上平移6个单位得到函数h1(x)的图象，试确定函数y＝g(x)－h1(x)的零点个数，并说明理由.
已知sinα＋cosα＝
，α∈(0，
)，sin(β－)＝
，β∈(，
)．
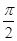(1) 求sin2α和tan2α的值；
(2) 求cos(α＋2β)的值．
设集合A为函数f(x)＝ln(－x2－2x＋8)的定义域，集合B为不等式(ax－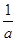
)(x＋4)≤0的解集．
(1) 写出f(x)的单调区间；
(2) 若B⊆∁R A，求a的取值范围．
现向图中所示正方形随机地投掷飞镖，求飞镖落在阴影部分的概率。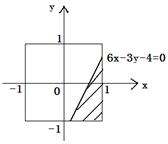
为了了解高一学生的体能状况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图），图中从左到右各小长方形的面积之比为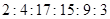
，第二小组频数为12．
（1）第二小组的频率是多少？
（2）样本容量是多少？
（3）若次数在110以上为达标，试估计全体高一学生的达标率为多少？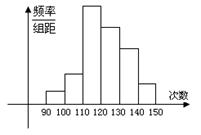
从甲、乙两名学生中选拔一人参加射击比赛，对他们的射击水平进行了测试，两人在相同条件下各射击10次，命中的环数如下:
| 甲 |
7 |
8 |
6 |
8 |
6 |
5 |
9 |
10 |
7 |
4 |
| 乙 |
9 |
5 |
7 |
8 |
7[ |
6 |
8 |
6 |
7 |
7 |
（1）计算甲乙两人射击命中环数的平均数和方差；
（2）比较两人的成绩，然后决定选择哪一人参赛