(1)已知角α的终边经过点P(3,4),求角α的六个三角函数值;
(2)已知角α的终边经过点P(3t,4t),t≠0,求角α的六个三角函数值.
已知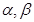 均为锐角,且
均为锐角,且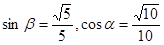 ,求
,求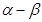 的值。
的值。
已知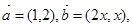
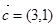 ,且
,且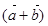 ∥
∥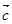 ,求实数x的值。
,求实数x的值。
(本小题满分14分) 函数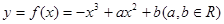 .
.
(1)要使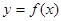 在(0,1)上单调递增,求
在(0,1)上单调递增,求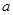 的取值范围;
的取值范围;
(2)当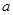 >0时,若函数满足
>0时,若函数满足 =1,
=1, =
=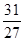 ,求函数
,求函数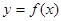 的解析式;
的解析式;
(3)若x∈[0,1]时,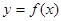 图象上任意一点处的切线倾斜角为θ,求当0≤θ≤
图象上任意一点处的切线倾斜角为θ,求当0≤θ≤ 时
时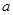 的取值范围.
的取值范围.
(本小题满分13分)已知点P(一1,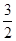 )是椭圆E:
)是椭圆E: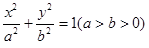 上一点F1,F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
上一点F1,F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
(1)求椭圆E的方程;
(2)设A,B是椭圆E上两个动点,满足: ,求直线AB的斜率
,求直线AB的斜率
(本小题满分12分)某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如下图所示.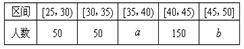

(1)上表是年龄的频数分布表,求正整数 的值;
的值;
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.