(本小题满分12分)某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如下图所示.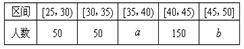

(1)上表是年龄的频数分布表,求正整数 的值;
的值;
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
已知等差数列
满足:
,
的前n项和为
.
(Ⅰ)求
及
;
(Ⅱ)令bn=
(n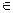 N*),求数列
的前n项和
.
N*),求数列
的前n项和
.
已知函数
,其图象过点
.
(Ⅰ)求
的值;
(Ⅱ)将函数
的图象上各点的横坐标缩短到原来的
,纵坐标不变,得到函数
的图象,求函数
在
上的最大值和最小值.
品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出
瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这
瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮 测试中的两次排序的偏离程度的高低为其评为。
测试中的两次排序的偏离程度的高低为其评为。
现设
,分别以
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
,则
是对两次排序的偏离程度的一种描述。
(Ⅰ)写出
的可能值集合;
(Ⅱ)假设
等可能地为1,2,3,4的各种排列,求
的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中,都有
,
(i)试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);
(ii)你认为该品酒师的酒味鉴别功能如何?说明理由。
设数列
中的每一项都不为0.
证明:
为等差数列的充分必要条件是:对任何
,都有
.
已知椭圆
经过点
,对称轴为坐标轴,焦点
在
轴上,离心率
。
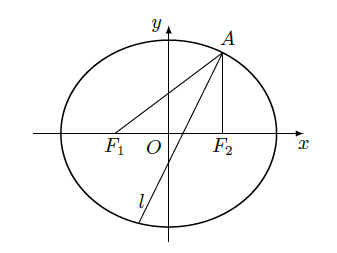
(Ⅰ)求椭圆
的方程;
(Ⅱ)求
的角平分线所在直线
的方程;
(Ⅲ)在椭圆
上是否存在关于直线
对称的相异两点?若存在,请找出;若不存在,说明理由。