作出函数y=|tanx|的图象,并根据图象求其单调区间
如图,某污水处理厂要在一个矩形 的池底水平铺设污水净化管道(直角
的池底水平铺设污水净化管道(直角 ,
, 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口 是
是 的中点,
的中点, 分别落在
分别落在
 上,且
上,且 ,设
,设 .
.
(1)试将污水管道的长度 表示成
表示成 的函数,并写出定义域;
的函数,并写出定义域;
(2)当管道长度 为何值时,污水净化效果最好,并求此时管道的长度.
为何值时,污水净化效果最好,并求此时管道的长度.
如图,已知正四棱柱 中,底面边长
中,底面边长 ,侧棱
,侧棱 的长为4,过点
的长为4,过点 作
作 的垂线交侧棱
的垂线交侧棱 于点
于点 ,交
,交 于点
于点 .
.
(1)求证: ⊥平面
⊥平面 ;
;
(2)求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
已知函数 .
.
(1)求函数 的零点,并求反函数
的零点,并求反函数 ;
;
(2)设 ,若不等式
,若不等式 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的范围.
的范围.
(本小题满分10分)(选修4—5:不等式选讲)
(Ⅰ)证明柯西不等式: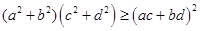 ;
;
(Ⅱ)若 且
且 ,用柯西不等式求
,用柯西不等式求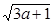 +
+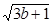 的最大值.
的最大值.
(本小题满分10分)选修4-4:坐标系与参数方程
将圆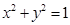 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线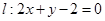 与C的交点为
与C的交点为 ,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段 的中点且与
的中点且与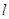 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.