某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元,该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元,假设商店每月购进这种商品m件,且当月销完,你估计哪个月份盈利最大?
已知函数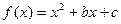 (其中
(其中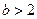 )且
)且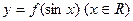 的最大值为
的最大值为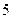 ,最小值为
,最小值为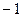 .
.
(1)求函数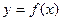 的解析式;
的解析式;
(2)是否存在最小的负数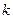 ,使得在整个区间
,使得在整个区间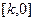 上不等式
上不等式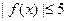 恒成立,若存在,求出
恒成立,若存在,求出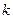 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若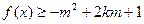 ,对所有
,对所有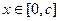 ,
,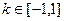 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知x=-1是 的一个极值点
的一个极值点
(1)求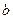 的值;
的值;
(2)求函数 的单调增区间;
的单调增区间;
(3)设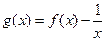 ,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由。
,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由。
已知函数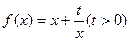 和点
和点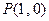 ,过点
,过点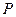 作曲线
作曲线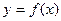 的两条切线
的两条切线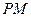 、
、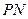 ,切点分别为
,切点分别为 、
、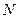 .
.
(Ⅰ)设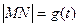 ,试求函数
,试求函数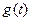 的表达式;
的表达式;
(Ⅱ)是否存在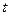 ,使得
,使得 、
、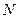 与
与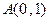 三点共线.若存在,求出
三点共线.若存在,求出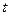 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数 ,在区间
,在区间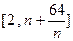 内总存在
内总存在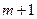 个实数
个实数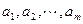 ,
,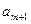 ,使得不等式
,使得不等式 成立,求
成立,求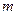 的最大值.
的最大值.
若存在实常数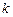 和
和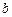 ,使得函数
,使得函数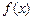 和
和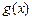 对其定义域上的任意实数
对其定义域上的任意实数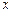 分别满足:
分别满足: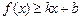 和
和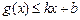 ,则称直线
,则称直线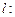
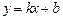 为
为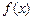 和
和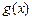 的“隔离直线”.已知
的“隔离直线”.已知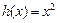 ,
,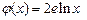 (其中
(其中 为自然对数的底数).
为自然对数的底数).
(1)求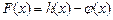 的极值;
的极值;
(2) 函数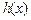 和
和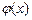 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
已知直线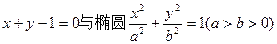 相交于A、B两点,M是线段AB上的一点,
相交于A、B两点,M是线段AB上的一点,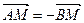 ,且点M在直线
,且点M在直线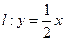 上.
上.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若椭圆的焦点关于直线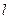 的对称点在单位圆
的对称点在单位圆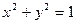 上,求椭圆的方程.
上,求椭圆的方程.