在平面直角坐标系中,O为坐标原点,已知点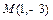 ,
,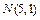 ,
,
若点C满足 ,点C的轨迹与抛物线
,点C的轨迹与抛物线 交于A、B两点.
交于A、B两点.
(I)求证: ;
;
(II)在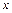 轴正半轴上是否存在一定点
轴正半轴上是否存在一定点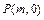 ,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
设函数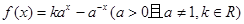 ,
,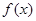 是定义域为R上的奇函数.
是定义域为R上的奇函数.
(1)求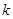 的值,并证明当
的值,并证明当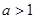 时,函数
时,函数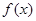 是R上的增函数;
是R上的增函数;
(2)已知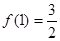 ,函数
,函数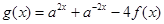 ,
, ,求
,求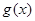 的值域;
的值域;
(3)若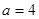 ,试问是否存在正整数
,试问是否存在正整数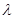 ,使得
,使得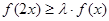 对
对 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数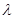 ;若不存在,请说明理由.
;若不存在,请说明理由.
如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,正方形ABCD的边长为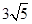 .
.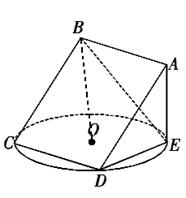
(1)求证:平面ABCD丄平面ADE;
(2)求四面体BADE的体积;
(3)试判断直线OB是否与平面CDE垂直,并请说明理由.
已知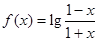 .
.
(1)求函数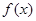 的定义域;
的定义域;
(2)判断并证明函数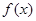 的奇偶性;
的奇偶性;
(3)若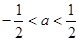 ,试比较
,试比较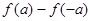 与
与 的大小.
的大小.
如图,在三棱柱ABC-A1B1C1中, CC1⊥底面ABC,AC=BC,M,N分别是CC1,AB的中点.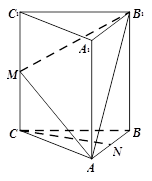
(1)求证:CN⊥AB1;
(2)求证:CN//平面AB1M.
设p;函数 在
在 上是增函数,q:函数
上是增函数,q:函数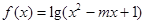 的定义域为R.
的定义域为R.
(1)若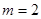 ,试判断命题p的真假;
,试判断命题p的真假;
(2)若命题p与命题q一真一假,试求实数 的取值范围.
的取值范围.