如图,在三棱柱ABC-A1B1C1中, CC1⊥底面ABC,AC=BC,M,N分别是CC1,AB的中点.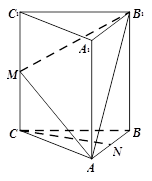
(1)求证:CN⊥AB1;
(2)求证:CN//平面AB1M.
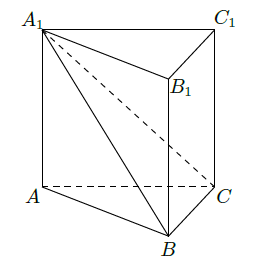
如图,在直三棱柱
中,平面
.
(Ⅰ)求证:
.
(Ⅱ)若
,直线
与平面
所成的角为
,二面角
的大小为
,求证:
. 
已知函数
(
为常数,且
)有极大值9.
(Ⅰ)求
的值;
(Ⅱ)若斜率为-5的直线是曲线
的切线,求此直线方程.
已知函数 .
(Ⅰ)将函数 化简成 求 的周期;
(Ⅱ)求函数 ;在 上的最大值和最小值.
已知数列
:
(
是正整数),与数列
:
(
是正整数).记
.
(1)若
,求
的值;
(2)求证:当
是正整数时,
;
(3)已知
,且存在正整数
,使得在
中有4项为100.求
的值,并指出哪4项为100.
已知双曲线
.
(1)求双曲线
的渐近线方程;
(2)已知点M的坐标为
.设
是双曲线
上的点,
是点
关于原点的对称点.记
.求
的取值范围;
(3)已知点
的坐标分别为
,
为双曲线
上在第一象限内的点.记
为经过原点与点
的直线,
为
截直线
所得线段的长.试将
表示为直线
的斜率k的函数.