如图，直角梯形ABCE中，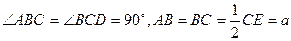
，D是CE的中点，点M和点N在
ADE绕AD向上翻折的过程中，分别以
的速度，同时从点A和点B沿AE和BD各自匀速行进，t 为行进时间，0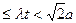
。
（1） 求直线AE与平面CDE所成的角；
（2） 求证：MN//平面CDE。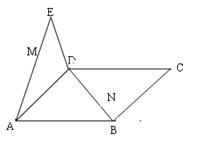
（本小题满分12分）
如图所示，已知S是正三角形ABC所在平面外的一点，且SA=SB=SC，SG为△SAB上的高，D、E、F分别是AC、BC、SC的中点，试判断SG与平面DEF的位置关系，并给予证明.
（本小题满分10分）
已知函数
(1）求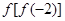
的值；
(2）当
时，求函数
的值域。
如图，已知三棱锥O－ABC的侧棱OA，OB，OC两两垂直，且OA=2，OB=3，OC=4，E是OC的中点．
（1）求异面直线BE与AC所成角的余弦值；
（2）求二面角A－BE－C的余弦值．
已知曲线
，直线
（1）将直线
的极坐标方程化为直角坐标方程；
（2）设点
在曲线
上，求点到直线的距离的最小值。
设矩阵
是把坐标平面上的点的横坐标伸长到3倍，纵坐标伸长到2倍的伸压变换矩阵．
（1）求逆矩阵
；
（2）求椭圆
在矩阵作用下变换得到的新曲线的方程．