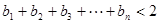已知常数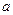 、
、 、
、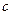 都是实数,函数
都是实数,函数 的导函数为
的导函数为
(Ⅰ)设 ,求函数
,求函数 的解析式;
的解析式;
(Ⅱ)如果方程 的两个实数根分别为
的两个实数根分别为 、
、 ,并且
,并且
问:是否存在正整数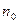 ,使得
,使得 ?请说明理由.
?请说明理由.
已知数列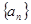 满足
满足 ,
,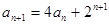
 .
.
(1)令 ,求证:数列
,求证:数列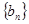 为等比数列;
为等比数列;
(2)求数列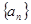 的通项公式;
的通项公式;
(3)求满足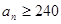 的最小正整数
的最小正整数 .
.
设关于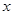 的不等式
的不等式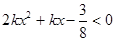 的解集为
的解集为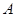 .
.
(1)若 ,求实数
,求实数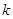 的取值范围;
的取值范围;
(2)求 ,求实数
,求实数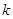 的取值范围.
的取值范围.
在数列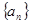 中,
中, ,
, .
.
(1)求出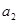 、
、 、
、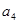 的值;
的值;
(2)求证:数列 为等差数列.
为等差数列.
(3)求数列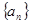 的通项公式.
的通项公式.
某厂用10万元新购一台生产设备,投入运行后每年需要管理费固定为9千元,同时还需要设备维修和养护,第一年维修和养护费需要2千元,以后每年的维修和养护费成等差数额在递增,第二年需要4千元,第三年需要6千元,…,问这种生产设备使用多少年报废最合算(即使用多少年的年平均费用最低)?
等差数列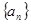 的前
的前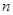 项之和为
项之和为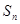 ,
,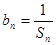 ,且
,且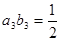 ,
,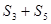
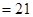 .
.
(1)求数列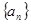 的通项公式;
的通项公式;
(2)求数列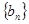 的通项公式;
的通项公式;
(3)求证: