某市旅游部门开发一种旅游纪念品,每件产品的成本是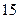 元,销售价是
元,销售价是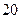 元,月平均销售
元,月平均销售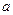 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为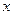
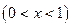 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为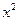 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是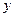 (元).
(元).
(Ⅰ)写出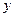 与
与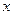 的函数关系式;
的函数关系式;
(Ⅱ)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.
已知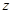 是复数,若
是复数,若 为实数(
为实数(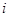 为虚数单位),且
为虚数单位),且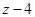 为纯虚数.
为纯虚数.
(1)求复数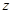 ;
;
(2)若复数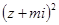 在复平面上对应的点在第四象限,求实数
在复平面上对应的点在第四象限,求实数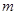 的取值范围
的取值范围
(本小题满分12分)已知椭圆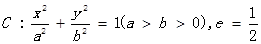 ,其中
,其中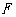 是椭圆的右焦点,焦距为2,直线
是椭圆的右焦点,焦距为2,直线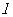 与椭圆
与椭圆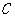 交于点
交于点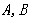 ,点
,点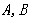 的中点横坐标为
的中点横坐标为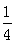 ,且
,且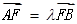 (其中
(其中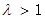 ).
).
(1)求椭圆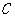 的标准方程;
的标准方程;
(2)求实数 的值.
的值.
【改编】已知函数f(x)=(x+1)lnx-x+1.
(1)若xf′(x)≤x2+ax+1,求a的取值范围;
(2)证明:当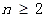 时,
时,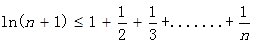 ;
;
某社团组织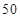 名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,倡导文明新风;2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下2
名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,倡导文明新风;2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下2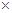 2的列联表所示:
2的列联表所示:
| 宣传慰问 |
义工 |
总计 |
|
| 20至40岁 |
16 |
||
| 大于40岁 |
15 |
23 |
|
| 总计 |
24 |
50 |
(1)填上表中所空缺的数值。
(2)分层抽样方法在做义工的志愿者中随机抽取6名,年龄在20至40岁与大于40岁的应该各抽取几名?
(3)根据(2)抽取的6名志愿者中任取2名,求选取的2人中分别来自上述年龄段各1人的概率。
已知复数z=1﹣i(i是虚数单位)
(Ⅰ)计算z2;
(Ⅱ)若z2+a ,求实数a,b的值.
,求实数a,b的值.