如图,平面ACB⊥平面BCD,∠CAB=∠CBD=900, ∠BDC=600,BC=6,AB=AC.
(Ⅰ)求证:平面ABD⊥平面ACD;(Ⅱ)求二面角A—CD—B的平面角的正切值;
(Ⅲ)设过直线AD且与BC平行的平面为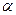 ,求点B到平面
,求点B到平面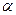 的距离。
的距离。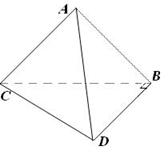
如图,AB是圆O的直径,C,D是圆O上两点,AC与BD相交于点E,GC,GD是圆O的切线,点F在DG的延长线上,且 。求证:
。求证:
(Ⅰ)D、E、C、F四点共圆;(Ⅱ)

已知 在
在 处取得极值。
处取得极值。
(Ⅰ)证明: ;
;
(Ⅱ)是否存在实数 ,使得对任意
,使得对任意 ?若存在,求
?若存在,求 的所有值;若不存在,说明理由。
的所有值;若不存在,说明理由。
四边形ABCD的四个顶点都在抛物线 上,A,C关于
上,A,C关于 轴对称,BD平行于抛物线在点C处的切线。
轴对称,BD平行于抛物线在点C处的切线。
(Ⅰ)证明:AC平分 ;
;
(Ⅱ)若点A坐标为 ,四边形ABCD的面积为4,求直线BD的方程。
,四边形ABCD的面积为4,求直线BD的方程。
如图,六棱锥 的底面是边长为1的正六边形,
的底面是边长为1的正六边形, 底面
底面 。
。
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)若直线PC与平面PDE所成角的正弦值为 ,求六棱锥
,求六棱锥 高的大小。
高的大小。
某经销商试销A、B两种商品一个月(30天)的记录如下:
| 日销售量(件) |
0 |
1 |
2 |
3 |
4 |
5 |
| 商品A的频数 |
3 |
5 |
7 |
7 |
5 |
3 |
| 商品B的频数 |
4 |
4 |
6 |
8 |
5 |
3 |
若售出每种商品1件均获利40元,用 表示售出A、B商品的日利润值(单位:元).将频率视为概率.
表示售出A、B商品的日利润值(单位:元).将频率视为概率.
(Ⅰ)设两种商品的销售量互不影响,求两种商品日获利值均超过100元的概率;
(Ⅱ)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由.