如图，三棱锥P—ABC中， PC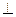
平面ABC，PC=AC=2，AB=BC，D是PB上一点，且CD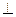平面PAB．
(I) 求证：AB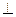平面PCB；
(II) 求异面直线AP与BC所成角的大小；
（III）求二面角C-PA-B的大小．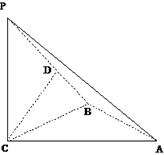
已知等差数列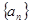
的公差
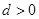，其前n项和为
,
,
；
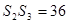（1）求出数列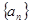的通项公式
及前n项和公式
（2）若数列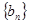
满足
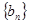，求数列的通项公式
已知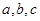
分别为△ABC三个内角A，B，C的对边，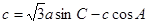
（1）求A
（2）若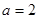
，△ABC的面积为
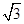，求b,c
已知：命题p：曲线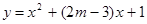
与
轴相交于不同的两点；
命题
表示焦点在
轴上的椭圆．
若“p且q” 是假命题，“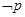
”是假命题，求
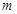取值范围．
如图，梯形ABCD的底边AB在y轴上，原点O为AB的中点，
M为CD的中点．
（Ⅰ）求点M的轨迹方程；
（Ⅱ）过M作AB的垂线，垂足为N，若存在正常数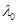
，使
，且P点到A、B 的距离和为定值，求点P的轨迹E的方程；
（Ⅲ）过
的直线与轨迹E交于P、Q两点，求
面积的最大值．
（本小题满分12分）数列
记
（Ⅰ）求b1、b2、b3、b4的值；
（Ⅱ）求数列
的通项公式及数列
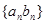的前n项和