(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
已知以原点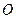 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为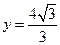 ,离心率
,离心率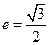 ,
,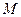 是椭圆上的动点。
是椭圆上的动点。
(Ⅰ)若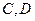 的坐标分别是
的坐标分别是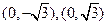 ,求
,求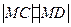 的最大值;
的最大值;
(Ⅱ)如题(20)图,点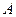 的坐标为
的坐标为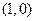 ,
,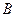 是圆
是圆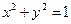 上的点,
上的点,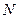 是点
是点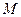 在
在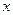 轴上的射影,点
轴上的射影,点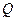 满足条件:
满足条件: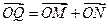 ,
,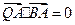 ,求线段
,求线段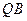 的中点
的中点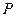 的轨迹方程。
的轨迹方程。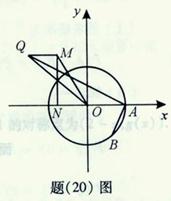
(本题15分)已知函数 是奇函数,且图像在点
是奇函数,且图像在点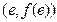
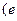 为自然对数的底数)处的切线斜率为3.
为自然对数的底数)处的切线斜率为3.
(1)求实数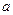 、
、 的值;
的值;
(2)若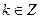 ,且
,且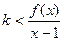 对任意
对任意 恒成立,求
恒成立,求 的最大值;
的最大值;
(3)当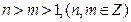 时,证明:
时,证明:
(本题15分)已知函数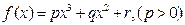 图象的对称中心为
图象的对称中心为 ,且
,且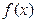 的极小值为
的极小值为 .
.
(1)求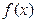 的解析式;
的解析式;
(2)设 ,若
,若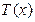 有三个零点,求实数
有三个零点,求实数 的取值范围;
的取值范围;
(3)是否存在实数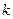 ,当
,当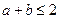 时,使函数
时,使函数
在定义域[a,b] 上的值域恰为[a,b],若存在,求出k的范围;若不存在,说明理由.
(本题14分)数列 的前
的前 项和为
项和为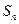 ,已知
,已知
(1)证明:数列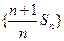 是等差数列,并求
是等差数列,并求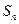 ;
;
(2)设 ,求证:
,求证: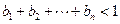 .
.
(本题14分)(如右图)半径为1,圆心角为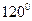 的扇形,点
的扇形,点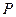 是扇形AB弧上的动点,设
是扇形AB弧上的动点,设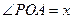 .
.
(1)用x表示平行四边形ODPC的面积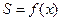 ;
;
(2)求平行四边形ODPC面积的最大值.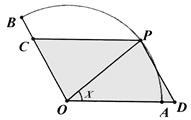
(本题14分)设集合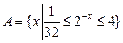 ,
,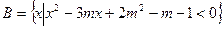
(1)当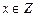 时,求A的非空真子集的个数
时,求A的非空真子集的个数
(2)若 ,求实数m的取值范围.
,求实数m的取值范围.