(本小题满分14分)已知函数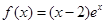 和
和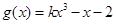 .
.
(Ⅰ)若函数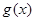 在区间
在区间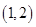 不单调,求实数
不单调,求实数 的取值范围;
的取值范围;
(Ⅱ)当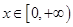 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
如图,已知正方体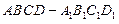 的棱长为2,E、F分别是
的棱长为2,E、F分别是 、
、 的中点,过
的中点,过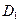 、E、F作平面
、E、F作平面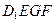 交
交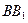 于G..
于G..
(Ⅰ)求证: ∥
∥ ;
;
(Ⅱ)求二面角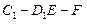 的余弦值;
的余弦值;
(Ⅲ)求正方体被平面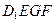 所截得的几何体
所截得的几何体 的体积.
的体积.
已知数列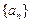 满足:
满足: 且
且 .
.
(Ⅰ)求 ,
, ,
, ,
, 的值及数列
的值及数列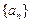 的通项公式;
的通项公式;
(Ⅱ)设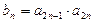 ,求数列
,求数列 的前
的前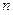 项和
项和 ;
;
在四棱锥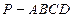 中,
中, ,
,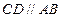 ,
, 底面
底面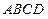 ,
, 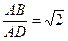 ,直线
,直线 与底面
与底面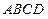 成
成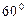 角,点
角,点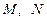 分别是
分别是 的中点.
的中点.
(1)求二面角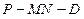 的大小;
的大小;
(2)当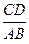 的值为多少时,
的值为多少时, 为直角三角形.
为直角三角形.
 如图,已知正三棱柱
如图,已知正三棱柱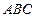 —
— 的底面边长是
的底面边长是 ,
,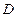 是侧棱
是侧棱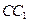 的中点,直线
的中点,直线 与侧面
与侧面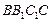 所成的角为
所成的角为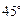 .
.
(Ⅰ)求此正三棱柱的侧棱长;
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.
一种电脑屏幕保护画面,只有符号“○”和“×”随机地反复出现,每秒钟变化一次,每次变化只出现“○”和“×”之一,其中出现“○”的概率为p,出现“×”的概率为q,若第k次出现“○”,则记 ;出现“×”,则记
;出现“×”,则记 ,令
,令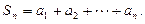
(I)当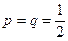 时,记
时,记 ,求
,求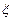 的分布列及数学期望;
的分布列及数学期望;
(II)当 时,求
时,求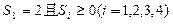 的概率.
的概率.