设函数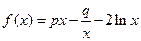 ,且
,且 ,其中
,其中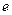 是自然对数的底数.
是自然对数的底数.
(1)求 与
与 的关系; (2)若
的关系; (2)若 在其定义域内为单调函数,求
在其定义域内为单调函数,求 的取值范围; (3)设
的取值范围; (3)设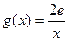 ,若在
,若在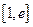 上至少存在一点
上至少存在一点 ,使得
,使得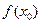 >
> 成立,求实数
成立,求实数 的取值范围.
的取值范围.
如图,从椭圆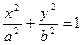
 上一点
上一点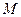 向
向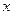 轴作垂线,恰好通过椭圆的左焦点
轴作垂线,恰好通过椭圆的左焦点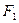 ,且它的长轴端点
,且它的长轴端点 及短轴端点
及短轴端点 的连线
的连线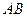 平行于
平行于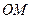 ,
,
(1)求椭圆的离心率;
(2)设 是椭圆上任意一点,
是椭圆上任意一点,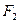 是右焦点,求
是右焦点,求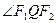 的取值范围;
的取值范围;
(3)设 是椭圆上一点,当
是椭圆上一点,当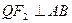 时,延长
时,延长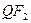 与椭圆交于另一点
与椭圆交于另一点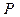 ,若
,若 的面积为
的面积为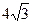 ,求此时的椭圆方程。
,求此时的椭圆方程。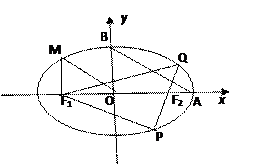
如图,在底面是矩形的四棱锥 中,
中, ,
, .
.
(1)求证:平面 ;
;
(2)若 为
为 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)在 上是否存在一点
上是否存在一点 ,使得
,使得 到平面
到平面 的距离为1?若存在,求出
的距离为1?若存在,求出 ,若不存在,请说明理由。
,若不存在,请说明理由。
若动点 到定点
到定点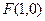 的距离比到直线
的距离比到直线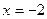 距离小1,求点
距离小1,求点 的轨迹方程。
的轨迹方程。
已知正方体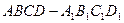 ,
, 是底面
是底面 对角线的交点,
对角线的交点,
(1)求证: //面
//面 ;
;
(2)求二面角 的正切值。
的正切值。
设 ,
, ,若
,若 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。