如图,在底面是矩形的四棱锥 中,
中, ,
, .
.
(1)求证:平面 ;
;
(2)若 为
为 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)在 上是否存在一点
上是否存在一点 ,使得
,使得 到平面
到平面 的距离为1?若存在,求出
的距离为1?若存在,求出 ,若不存在,请说明理由。
,若不存在,请说明理由。
已知数列 是各项均不为0的等差数列,公差为d,
是各项均不为0的等差数列,公差为d,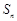 为其前n项和,且满足
为其前n项和,且满足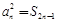 ,
,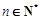 .数列
.数列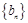 满足
满足 ,
,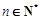 ,
, 为数列
为数列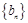 的前n项和.
的前n项和.
(1)求数列 的通项公式
的通项公式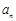 和数列
和数列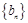 的前n项和
的前n项和 ;
;
(2)若对任意的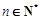 ,不等式
,不等式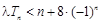 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)是否存在正整数
 ,使得
,使得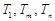 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知曲线 上动点
上动点 到定点
到定点 与定直线
与定直线 的距离之比为常数
的距离之比为常数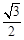 .
.
(1)求曲线 的轨迹方程;
的轨迹方程;
(2)若过点 引曲线C的弦AB恰好被点
引曲线C的弦AB恰好被点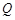 平分,求弦AB所在的直线方程;
平分,求弦AB所在的直线方程;
(3)以曲线 的左顶点
的左顶点 为圆心作圆
为圆心作圆 :
: ,设圆
,设圆 与曲线
与曲线 交于点
交于点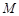 与点
与点 ,求
,求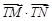 的最小值,并求此时圆
的最小值,并求此时圆 的方程.
的方程.
某省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数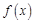 与时刻
与时刻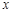 (时) 的关系为
(时) 的关系为 ,其中
,其中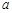 是与气象有关的参数,且
是与气象有关的参数,且 .
.
(1)令 ,
, 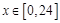 ,写出该函数的单调区间,并选择其中一种情形进行证明;
,写出该函数的单调区间,并选择其中一种情形进行证明;
(2)若用每天 的最大值作为当天的综合放射性污染指数,并记作
的最大值作为当天的综合放射性污染指数,并记作 ,求
,求 ;
;
(3)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染指数是否超标?
已知函数 .]
.]
(1)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(2)设 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 ,
, ,
, ,且
,且 ,
, ,
,
若 ,求
,求 ,
, 的值.
的值.
如图,已知四棱锥 的底面ABCD为正方形,
的底面ABCD为正方形, 平面ABCD,E、F分别是BC,PC的中点,
平面ABCD,E、F分别是BC,PC的中点, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求二面角 的大小.
的大小.