在直角坐标系
中,椭圆
:
的左、右焦点分别为
.
也是抛物线
:
的焦点,点
为
与
在第一象限的交点,且
.
(Ⅰ)求
的方程;
(Ⅱ)平面上的点
满足
,直线
,且与
交于
两点,若
,求直线
的方程.
为了了解某班的男女生学习体育的情况,按照分层抽样分别抽取了10名男生和5名女生作为样本,他们期末体育成绩的茎叶图如图所示,其中茎为十位数,叶为个位数。
(Ⅰ)若该班男女生平均分数相等,求x的值;
(Ⅱ)若规定85分以上为优秀,在该10名男生中随机抽取2名,优秀的人数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
已知函数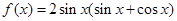 .
.
(Ⅰ)求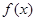 的最小正周期;
的最小正周期;
(Ⅱ)当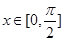 时,求
时,求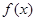 的最大值.
的最大值.
已知函数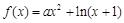 .
.
(1)当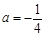 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)当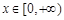 时,不等式
时,不等式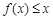 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(Ⅲ)求证: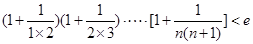 (
( ,e是自然对数的底数).
,e是自然对数的底数).
提示: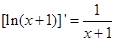
已知数列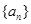 的前
的前 项和
项和 ,满足:
,满足: .
.
(Ⅰ)求数列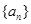 的通项
的通项 ;
;
(Ⅱ)若数列 的满足
的满足 ,
,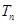 为数列
为数列 的前
的前 项和,求证:
项和,求证: .
.
如图,在长方体 中,
中,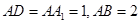 ,点E为AB的中点.
,点E为AB的中点.
(Ⅰ)求 与平面
与平面 所成的角;
所成的角;
(Ⅱ)求二面角 的平面角的正切值.
的平面角的正切值.