已知长方形ABCD, AB=2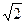 , BC="1." 以AB的中点
, BC="1." 以AB的中点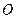 为原点建立如图8所示的平面直角坐标系
为原点建立如图8所示的平面直角坐标系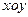 .
.
(Ⅰ)求以A、B为焦点,且过C、D两点的椭圆的标准方程;
(Ⅱ)过点P(0,2)的直线 交(Ⅰ)中椭圆于M,N两点,是否存在直线
交(Ⅰ)中椭圆于M,N两点,是否存在直线 ,使得以弦MN为直径的圆恰好过原点?若存在,求出直线
,使得以弦MN为直径的圆恰好过原点?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
设 集合
集合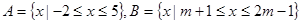 ,
,
(1)若 ,求实数
,求实数 的取值范围;
的取值范围;
(2)当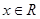 时,没有元素
时,没有元素 使得
使得 与
与 同时成立,求实数
同时成立,求实数 的取值范围。
的取值范围。
(本小题满分13分)已知函数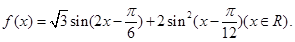
(1)求函数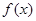 的最小正周期;
的最小正周期;
(2)求使函数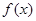 取得最大值的
取得最大值的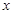 集合。
集合。
已知函数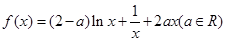
(1)当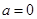 时,求
时,求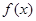 的极值
的极值
(2)当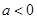 时,求
时,求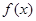 的单调区间
的单调区间
(3)若对任意的 ,恒
,恒 有
有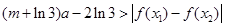 成立,求实数
成立,求实数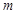 的取值范围。
的取值范围。
椭圆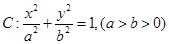 的离心率为
的离心率为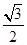 ,长轴的端点与短轴的端点间的距离为
,长轴的端点与短轴的端点间的距离为
(1)求椭圆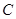 的方程
的方程
(2)设过点 的直线
的直线 与椭圆
与椭圆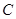 交于
交于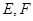 两点,
两点,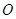
 为坐标原点,若△
为坐标原点,若△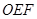 为
为 直角三角形,求直线
直角三角形,求直线 的斜率。
的斜率。
口袋里装有大小相同的卡片八张,其中三张标有数字1,三张标有数字2,二张标有数字3,第一次从口袋里任里任意抽取一张,放回口袋里后第二次再任意抽取一张,记第一次与第二次取到卡片上数字之和为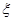 .
.
(1)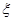 为何值时,其发生的概率最大?说明理由;
为何值时,其发生的概率最大?说明理由;
(2)求随机变量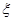 的期望
的期望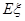 .
.