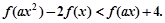如图，已知直线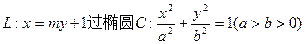
的右焦点F，且交椭圆C于A，B两点，点A，F，B在直线
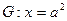上的射影依次为点D，K，E.
（1）若抛物线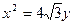
的焦点为椭圆C的上顶点，求椭圆C的方程；
（2）对于（1）中的椭圆C，若直线L交y轴于点M，且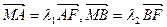
，当m变化时，求
的值；
（3）连接AE，BD，试探索当m变化时，直线AE、BD是否相交于一定点N？若交于定点N，请求出N点的坐标，并给予证明；否则说明理由.
将函数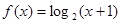
的图像向左平移1个单位，再将图像上的所
有点的纵坐标伸长到原来的2倍（横坐标不变），得到函数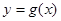
的图像.
（1）求函数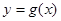的解析式和定义域；
（2）求函数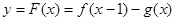
的最大值.
某海滨浴场的岸边可以近似的看成直线，位于岸边A处的救生员发现海
中B处有人求救，救生员没有直接从A处游向B处，而是沿岸边自A跑到距离B最近的D
处，然后游向B处.若救生员在岸边的行进速度是6米/秒，在海中的行进速度是2米/秒.
（不考虑水流速度等因素）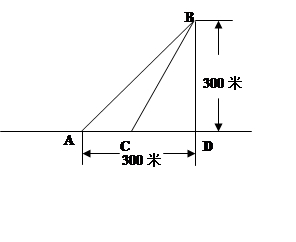
（1）请分析救生员的选择是否正确；
（2）在AD上找一点C，使救生员从A到B的时间最短，并求出最短时间.
已知关于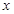
的不等式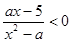
的解集为
.
(1)当
时，求集合；
（2）当
时,求实数
的范围.
已知函数
是偶函数．
（Ⅰ）求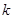
的值;
（Ⅱ）设
,若函数
与
的图象有且只有一个公共点,求
实数
的取值范围．
已知函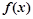数
对任意实数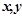
恒有
且当x＞0，
(1)判断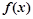的奇偶性；
(2)求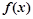在区间[－3,3]上的最大值；
(3)解关于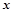
的不等式