（本小题满分10分）选修4—4；坐标系与参数方程．已知曲线：-优题课

（本小题满分10分）选修4—4；坐标系与参数方程．
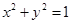已知曲线：，将曲线上的点按坐标变换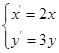得到曲线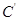；以直角坐标系原点为极点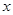，轴的正半轴为极轴建立极坐标系，直线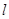的极坐标系方程是．
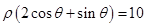（1）写出曲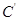线和直线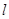的普通方程；
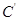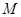（2）求曲线上的点到直线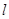距离的最大值及此时点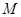的坐标．

科目数学题型解答题难度中等

知识点：参数方程

已知角的终边在直线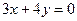上，求的值.

如图，过抛物线 $y^{2} = 2 p x (p > 0)$ 的焦点F的直线与抛物线相交于 $M$ 、 $N$ 两点，自 $M$ 、 $N$ 向准线L作垂线，垂足分别为 $M_{1}$ 、 $N_{1}$

(Ⅰ)求证： $F M_{1} ⊥ F M_{2}$ :
(Ⅱ)记 $∆ F M M_{1}$ _、 $∆ F M_{1} N_{1}$ 、 $∆ F N N_{1}$ 的面积分别为 $S_{1,} S_{2,} S_{3}$ ，试判断 ${S_{2}}^{2} = 4 S_{1} S_{2}$ 是否成立，并证明你的结论.

已知关于x的函数f(x)＝＋bx²＋cx＋bc,其导函数为f⁺(x).令g(x)＝∣f (x) ∣,记函数g(x)在区间[-1、1]上的最大值为M.
(Ⅰ)如果函数f(x)在x＝1处有极值-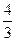，试确定b、c的值：
（Ⅱ）若∣b∣>1,证明对任意的c,都有M>2:
(Ⅲ)若M≧K对任意的b、c恒成立，试求k的最大值。

已知 $\{a_{n}\}$ 是一个公差大于0的等差数列，且满足 $a_{3} a_{6}$ ＝55, $a_{2} + a_{7}$ ＝16.
(Ⅰ)求数列 $\{a_{n}\}$ 的通项公式：
（Ⅱ）若数列 $\{a_{n}\}$ 和数列 $\{b_{n}\}$ 满足等式： $a_{n}$ _＝ $\frac{b_{1}}{2} + \frac{b_{2}}{2^{2}} + \frac{b_{3}}{2^{3}} + \dots \frac{b_{n}}{2^{n}} (n 为正整数)$ ，求数列 $\{b_{n}\}$ 的前 $n$ 项和 $S_{n}$

如图，四棱锥 $S ＝ A B C D$ 的底面是正方形， $S D ⊥$ 平面 $A B C D$ , $S D ＝ A D ＝ a$ ,点 $E 是 S D 上$ 的点，且 $D E ＝ λ a (0 < λ ≦ 1)$ .

(Ⅰ)求证：对任意的 $λ \in (0, 1)$ ，都有 $A C ⊥ B E$ :

(Ⅱ)若二面角 $C - A E - D$ 的大小为 $60 °$ ，求 $λ$ 的值.

试卷网试题网古诗词网作文网范文网