如图,四棱锥
的底面是正方形,
平面
,
,点
的点,且
 .
.

(Ⅰ)求证:对任意的 ,都有 :
(Ⅱ)若二面角 的大小为 ,求 的值.
附加题) 某电视台的一个智力游戏节目中,有一道将四本由不同作者所著的外国名著A、B、C、D与它们的作者连线的题目,每本名著只能与一名作者连线,每名作者也只能与一本名著连线。每连对一个得3分,连错得一1分,一名观众随意连线,他的得分记作X。
(1)求该观众得分非负的概率;
(2)求X的分布列及数学期望。
附加题) 如图所示,在直三棱柱ABC—A1B1C1中,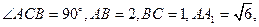 D是棱CC1的中点。
D是棱CC1的中点。
(1)证明:A1D⊥平面AB1C1;
(2)求二面角B—AB1—C1的余弦值;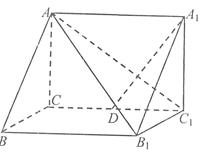
附加题) 已知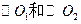 的极坐标方程分别是
的极坐标方程分别是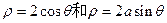 (a是常数).
(a是常数).
(1)分别将两个圆的极坐标方程化为直角坐标方程;
(2)若两个圆的圆心距为 的值。
的值。
附加题) 已知矩阵 ,
,
(1)计算AB;
(2)若矩阵B把直线 的方程。
的方程。
若存在实数k,b,使得函数 和
和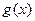 对其定义域上的任意实数x同时满足:
对其定义域上的任意实数x同时满足: ,则称直线:
,则称直线: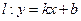 为函数
为函数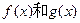 的“隔离直线”。已知
的“隔离直线”。已知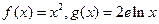 (其中e为自然对数的底数)。试问:
(其中e为自然对数的底数)。试问:
(1)函数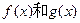 的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
(2)函数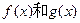 是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由。
是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由。