如图,A点在x轴上方,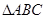 外接圆半径
外接圆半径 ,弦
,弦 在
在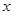 轴上且
轴上且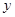 轴垂直平分
轴垂直平分 边,
边,
(1)求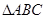 外接圆的标准方程
外接圆的标准方程
(2)求过点 且以
且以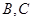 为焦点的椭圆方程
为焦点的椭圆方程
已知函数y=3sin
(1)用五点法在给定的坐标系中作出函数一个周期的图象;
(2)求此函数的振幅、周期和初相;
(3)求此函数图象的对称轴方程、对称中心.
在平面直角坐标系中,O为坐标原点,A、B、C三点满足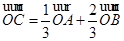
(1)求证:A、B、C三点共线;
(2)求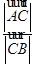 的值;
的值;
(3)已知 ,
,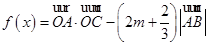 的最小值为
的最小值为 ,求实数m的值.
,求实数m的值.
已知向量 ,函数
,函数 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为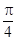 .
.
(1)求 的值;
的值;
(2)若 ,
, ,求
,求 的值;
的值;
(3)若 ,且
,且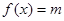 有且仅有一个实根,求实数
有且仅有一个实根,求实数 的值.
的值.
已知函数 为偶函数,其图象上相邻的两个最低点间的距离为
为偶函数,其图象上相邻的两个最低点间的距离为 .
.
(1)求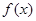 的解析式;
的解析式;
(2)若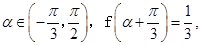 求
求 的值.
的值.
设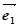 与
与 是两个单位向量,其夹角为60°,且
是两个单位向量,其夹角为60°,且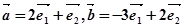 ,
,
(1)求
(2)分别求 的模;
的模;
(3)求 的夹角。
的夹角。