对某校全体教师在教学中是否经常使用信息技术实施教学的情况进行了调查,得到统计数据如下:
| 教师年龄 |
5年以下 |
5年至10年 |
10年至20年 |
20年以上 |
| 教师人数 |
8 |
10 |
30 |
18 |
| 经常使用信息技术实施教学的人数 |
2 |
4 |
10 |
4 |
(Ⅰ)求该校教师在教学中不经常使用信息技术实施教学的概率.
(Ⅱ)在教龄10年以下,且经常使用信息技术教学的教师中任选2人,其中恰有一人教龄在5年以下的概率是多少?
设函数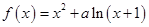
(1)若函数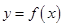 在区间
在区间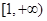 上是单调递增函数,求实数a的取值范围:
上是单调递增函数,求实数a的取值范围:
(2)若函数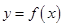 有两个极值点
有两个极值点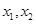 ,且
,且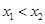 ,求证:
,求证:
已知椭圆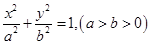 的离心率为
的离心率为 ,且过点
,且过点
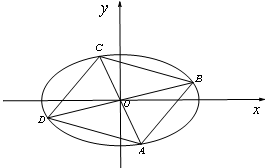
(1)求椭圆的标准方程:
(2)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,若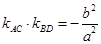
(ⅰ)求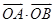 的最值:
的最值:
(ⅱ)求证:四边形ABCD的面积为定值.
数列 的各项均为正数,
的各项均为正数,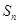 为其前n项和,对于任意的
为其前n项和,对于任意的 ,总有
,总有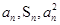 成等差数列
成等差数列
(1)求数列 的通项公式:
的通项公式:
(2)设数列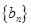 前n项和为
前n项和为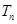 ,且
,且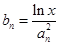 ,求证对任意的实数
,求证对任意的实数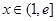 和任意的正整数n,总有
和任意的正整数n,总有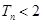 .
.
如图,四棱锥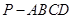 中,
中,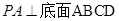 .
. ,F为PC的中点,
,F为PC的中点,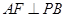 .
.
(1)求 的长:
的长:
(2)求二面角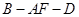 的正弦值.
的正弦值.