设椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、 ,A是椭圆C上的一点,且
,A是椭圆C上的一点,且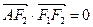 ,坐标原点O到直线
,坐标原点O到直线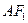 的距离为
的距离为 .
.
(1)求椭圆C的方程;
(2)设Q是椭圆C上的一点,过Q的直线l交x轴于点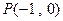 ,较y轴于点M,若
,较y轴于点M,若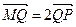 ,求直线l的方程.
,求直线l的方程.
( 12分)
已知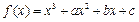 在
在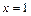 与
与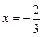 时都取得极值.
时都取得极值.
(Ⅰ)求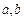 的值;
的值;
(Ⅱ)若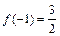 ,求
,求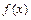 的单调区间和极值。
的单调区间和极值。
在⊿ABC中,BC=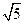 ,AC=3,sinC=2sinA
,AC=3,sinC=2sinA
(I) 求AB的值:
(II) 求sin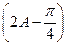 的值
的值
已知数列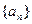 ,
,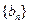 满足
满足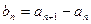 ,其中
,其中 .
.
(Ⅰ)若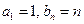 ,求数列
,求数列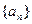 的通项公式;
的通项公式;
(Ⅱ)若 ,且
,且 .
.
(ⅰ)记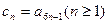 ,求证:数列
,求证:数列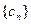 为等差数列;
为等差数列;
(ⅱ)若数列 中任意一项的值均未在该数列中重复出现无数次. 求首项
中任意一项的值均未在该数列中重复出现无数次. 求首项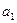 应满足的条件.
应满足的条件.
设函数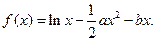
(Ⅰ)当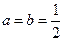 时,求
时,求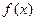 的最大值;
的最大值;
(Ⅱ)令 ,(
,(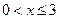 ),其图象上任意一点
),其图象上任意一点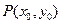 处切线的斜率
处切线的斜率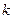 ≤
≤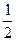 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)当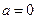 ,
,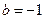 ,方程
,方程 有唯一实数解,求正数
有唯一实数解,求正数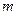 的值.
的值.
设椭圆C1: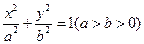 的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2:
的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2: 与y轴的交点为B,且经过F1,F2点.
与y轴的交点为B,且经过F1,F2点.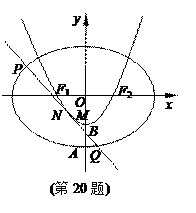
(Ⅰ)求椭圆C1的方程;
(Ⅱ)设M(0,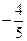 ),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求
),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求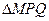 面积的最大值.
面积的最大值.