(本小题满分13分)
已知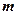
 ,
,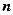
 ,其中
,其中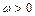 ,若函数
,若函数
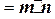 ,且
,且 的对称中心到
的对称中心到 对称轴的最近距离不小于
对称轴的最近距离不小于 (Ⅰ)求
(Ⅰ)求 的取值范围;(Ⅱ)在
的取值范围;(Ⅱ)在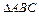 中,
中,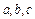 分别是角
分别是角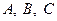 的对边,且
的对边,且 ,当
,当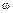 取最大值时,
取最大值时,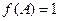 ,求
,求 的面积.
的面积.
在△ABC中,已知tanA=3,sinB= ,求角C的大小.
,求角C的大小.
在△ABC中,角A、B、C的对边分别为a、b、c,满足(c-2a)cosB+bcosC=0
(1)求角B的大小;


(2)若a=2,cosA= ,求c的值
,求c的值
(本题16分)已知方程x2+y2-2x-4y+m=0.
(1)若此方程表示圆,求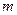 的取值范围;
的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M,N两点,且OM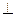 ON(O为坐标原点)求m的值;
ON(O为坐标原点)求m的值;
(3)在(2)的条件下,求以MN为直径的圆的方程.
如图,互相垂直的两条公路 、
、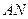 旁有一矩形花园
旁有一矩形花园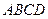 ,现欲将其扩建成一个更大的三角形花园
,现欲将其扩建成一个更大的三角形花园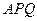 ,要求
,要求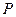 在射线
在射线 上,
上, 在射线
在射线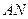 上,且
上,且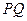 过点
过点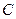 ,其中
,其中 米,
米,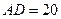 米. 记三角形花园
米. 记三角形花园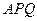 的面积为S.
的面积为S.
(Ⅰ)当 的长度是多少时,S最小?并求S的最小值.
的长度是多少时,S最小?并求S的最小值.
(Ⅱ)要使S不小于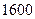 平方米,则
平方米,则 的长应在什么范围内?
的长应在什么范围内?
(本大题14分)如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
(1)求证:B1D1∥面EFG
(2)求证:平面AA1C⊥面EFG.