平行四边形ABCD中，AB=2，AD=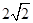
，且
，以BD为折线，把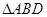
折起，使平面
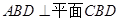，连AC。
（1）求异面直线AD与BC所成角大小；
（2）求二面角B-AC-D平面角的大小；
（3）求四面体ABCD外接球的体积。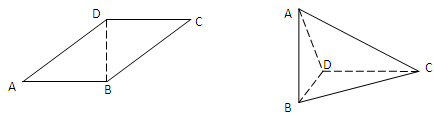
已知f（x）=
[3ln（x+2）-ln（x-2）]
（Ⅰ）求x为何值时，f（x）在[3，7]上取得最大值；
（Ⅱ）设F（x）=aln（x-1）－f（x），若F（x）是单调递增函数，求a的取值范围。
已知数列｛an｝的各项均是正数，其前n项和为sn，满足（p-1）sn=p2-an，其中p为正常数，且p≠1。
（Ⅰ）求数列｛an｝的通项公式：
（Ⅱ）设bn=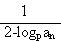
（n∈N※），数列｛bnbn+2｝的前n项和为Tn，求证：
Tn<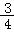
设A（x1，y1），B（x2，y2）是椭圆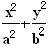
=1（a>b>0）上的两点，已知向量m(
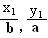) ,n(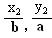
),若m·n=0且椭圆的离心率e=
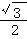，短轴长为2，O为坐标原点：
(Ⅰ)求椭圆的方程：
(Ⅱ)若直线AB过椭圆的焦点F(0,c)，(为半焦距)，求直线AB的斜k率的值：
(Ⅲ)试问：△AOB的面积是否为定值？
如图在直三棱柱ABC-A1B1C1中，∠ACB=90°2AC=AA1=BC=2。
（Ⅰ）若D为AA1中点，求证：平面B1CD⊥平面B1C1D；
（Ⅱ）若二面角B1－DC－C1的大小为60°，求AD 的长。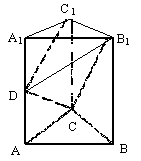
如图 A B两点有5条线并联，它们在单位时间内能通过的信息依次为2、3、4、3、2，现从中任取三条线且记在单位时间内通过的信息总量为ζ。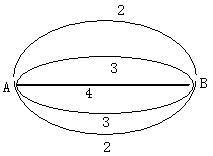
（Ⅰ）写出信息总量ζ的分布布列；
（Ⅱ）求信息总量ζ的数学期望。