(本小题满分12分)已知抛物线 的准线方程
的准线方程 ,
, 与直线
与直线 在第一象限相交于点
在第一象限相交于点 ,过
,过 作
作 的切线
的切线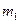 ,过
,过 作
作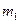 的垂线
的垂线 交x轴正半轴于点
交x轴正半轴于点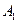 ,过
,过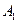 作
作 的平行线
的平行线 交抛物线
交抛物线 于第一象限内的点
于第一象限内的点 ,过
,过 作抛物线
作抛物线 的切线
的切线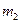 ,过
,过 作
作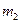 的垂线
的垂线 交x轴正半轴于点
交x轴正半轴于点 ,…,依此类推,在x轴上形成一点列
,…,依此类推,在x轴上形成一点列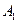 ,
, ,
, ,…,
,…, ,设点
,设点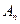 的坐标为
的坐标为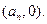
(Ⅰ)试探求 关于
关于 的递推关系式; (Ⅱ)求证:
的递推关系式; (Ⅱ)求证: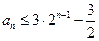 ;
;
(Ⅲ)求证: .
.
设 是定义在
是定义在 上的函数,若存在
上的函数,若存在
 ,使得
,使得 在
在 上单调递增,在
上单调递增,在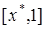 上单调递减,则称
上单调递减,则称 为
为 上的单峰函数,
上的单峰函数, 为峰点,包含峰点的区间为含峰区间. 对任意的
为峰点,包含峰点的区间为含峰区间. 对任意的 上的单峰函数
上的单峰函数 ,下面研究缩短其含峰区间长度的方法.
,下面研究缩短其含峰区间长度的方法.
(1)证明:对任意的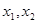
 ,
,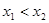 ,若
,若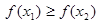 ,则
,则 为含峰区间;若
为含峰区间;若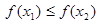 ,则
,则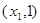 为含峰区间;
为含峰区间;
(2)对给定的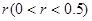 ,证明:存在
,证明:存在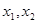
 ,满足
,满足 ,使得由(1)所确定的含峰区间的长度不大于
,使得由(1)所确定的含峰区间的长度不大于 ;
;
定义在R上的函数y=f(x),f(0)≠0,当x>0时,f(x)>1,且对任意的a、b∈R,有f(a+b)=f(a)f(b),
(1)求证:f(0)=1;
(2)求证:对任意的x∈R,恒有f(x)> 0;
(3)证明:f(x)是R上的增函数;(4)若f(x)·f(2x-x2)>1,求x的取值范围。
设函数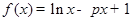
(Ⅰ)求函数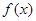 的极值点;(Ⅱ)当p>0时,若对任意的x>0,恒有
的极值点;(Ⅱ)当p>0时,若对任意的x>0,恒有 ,求p的取值范围;
,求p的取值范围;
(Ⅲ)证明:
已知二次函数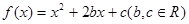 满足
满足 ,且关于
,且关于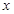 的方程
的方程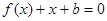 的两实数根分别在区间(-3,-2),(0,1)内。
的两实数根分别在区间(-3,-2),(0,1)内。
(1)求实数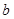 的取值范围;
的取值范围;
(2)若函数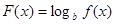 在区间(-1-
在区间(-1- ,1-
,1- )上具有单调性,求实数C的取值范围
)上具有单调性,求实数C的取值范围
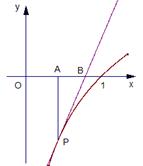
已知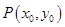 是函数
是函数 图象上一点,过点
图象上一点,过点 的切线与
的切线与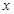 轴交于
轴交于 ,过点
,过点 作
作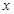 轴的垂线,垂足为
轴的垂线,垂足为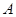 .
.
(1)求点 坐标;
坐标;
(2)若 ,求
,求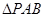 的面积
的面积 的最大值,并求此时
的最大值,并求此时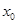 的值.
的值.