已知点
为圆周
的动点，过点作
轴，垂足为
，设线段
的中点为
，记点的轨迹方程为
，点
(1)求动点的轨迹方程;
(2)若斜率为
的另一个交点为
，求
面积的最大值及此时直线
的方程；
(3)是否存在方向向量
的直线
交与两个不同的点
，且有
？若存在，求出
的取值范围；若不存在，说明理由。
(本小题满分13分)
某建筑工地在一块长AM=30米，宽AN=20米的矩形地块AMPN上施工，规划建设占地如图中矩形ABCD的学生公寓，要求顶点C在地块的对角线MN上，B，D分别在边AM，AN上，假设AB长度为
米。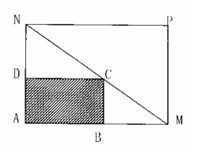
（1）要使矩形学生公寓ABCD的面积不小于144平方米，AB的长度应在什么范围？
（2）长度AB和宽度AD分别为多少米时矩形学生公寓ABCD的面积最大？最大值是多少平方米？
(本小题满分12分)
如图，在三棱柱ADF—BCE中，侧棱
底面
，底面是等腰直角三角形，且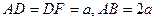
，M、G分别是AB、DF的中点. 
(1)求证GA∥平面FMC;
（2）求直线DM与平面ABEF所成角。
(本小题满分12分)
盒中有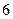
个小球,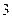
个白球,记为
，
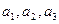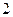个红球, 记为
，
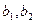个黑球, 记为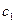
，除了颜色和编号外,球没有任何区别.
(1) 求从盒中取一球是红球的概率；
(2) 从盒中取一球，记下颜色后放回，再取一球，记下颜色，若取白球得分，取红球得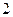分，取黑球得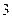分，求两次取球得分之和为
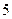分的概率
(本小题满分12分)
已知函数
．
（1）求函数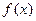
的最小正周期；
（2）当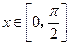
时，求函数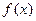的取值范围．
