若向量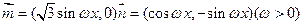
，在函数
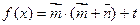的图象中，对称中心到对称轴的最小距离为
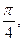且当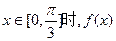
的最大值为1。
（I）求函数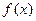
的解析式；
（II）求函数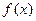的单调递增区间。
设函数f(x)＝lnx－ax，g(x)＝ex－ax，其中a为实数．
(1)若f(x)在(1，＋∞)上是单调减函数，且g(x)在(1，＋∞)上有最小值，求a的取值范围；
(2)若g(x)在(－1，＋∞)上是单调增函数，试求f(x)的零点个数，并证明你的结论．
设
.
（1）当
时，
，求a的取值范围；
（2）若对任意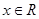
，
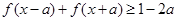恒成立，求实数a的最小值.
已知曲线C的极坐标方程为
，直线
的参数方程为
（t为参数，
）.
（1）把曲线C的极坐标方程化为直角坐标方程，并说明曲线C的形状；
（2）若直线经过点
，求直线被曲线C截得的线段AB的长.
如图，直线AB过圆心O，交
于F（不与B重合），直线
与相切于C，交AB于E，且与AF垂直，垂足为G，连结AC.
求证：（1）
；（2）
.
已知函数
.
（1）当
时，求
的极值；
（2）当
时，讨论的单调性；
（3）若对任意的
，
，恒有
成立，求实数
的取值范围.