盒中装有大小相等的球10个,编号分别为0,1,2,…,9,从中任取1个,观察号码是“小于5”“等于5”“大于5”三类情况之一.规定一个随机变量,并求其概率分布列.
选修4—4坐标系与参数方程
在直角坐标系中,以坐标原点为极点,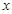 轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为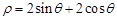 ,曲线D的参数方程为
,曲线D的参数方程为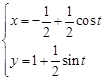 (
(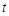 为参数).
为参数).
(Ⅰ)把C的极坐标方程化为直角坐标方程;
(Ⅱ)判定曲线C与曲线D间的位置关系.
选修4—1几何证明选讲
已知P是圆O外一点,PE切圆O于点E,A是圆O上一点,PA交圆O于B点,C为AE一点,PC交BE与D,CE=DE.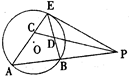
(Ⅰ)求证:PC是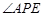 的平分线
的平分线
(Ⅱ)
(本小题满分12分)某校高三有800名同学参加学校组织的化学学科竞赛,其成绩的频率分布直方图如图所示,规定90分及其以上为获优胜奖.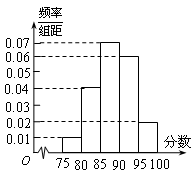
(Ⅰ)下表是这次考试成绩的频数分布表,求正整数a, b的值;
| 区间 |
[75,80) |
[80,85) |
[85,90) |
[90,95) |
[95,100] |
| 人数 |
40 |
a |
280 |
240 |
b |
(Ⅱ)现在要用分层抽样的方法从这800人中抽取5人参加某项活动,求其中获优胜奖的学生人数;
(Ⅲ)在(Ⅱ)中抽取的5名学生中,要随机选取2名学生参加市全省化学学科竞赛,求选取的两名学生中恰有含1名获优胜奖的概率.
(本小题满分12分)已知三棱锥 中,
中, ⊥面
⊥面 ,
, 是
是 的中点,
的中点,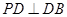 ,
,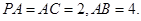
(Ⅰ)求证: ;
;
(Ⅱ)若 是
是 的中点,则平面
的中点,则平面 将三棱锥
将三棱锥 分成的两部分的体积之比.
分成的两部分的体积之比.
(本大题满分12分)已知{ }是公差
}是公差 ≠0的等差数列,
≠0的等差数列, ,
, ,
, 成等比数列,
成等比数列,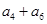 =26,数列{
=26,数列{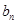 }是公比
}是公比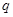 为正数的等比数列,且
为正数的等比数列,且 =
= ,
,  =
=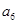 。
。
(Ⅰ)求数列{ },{
},{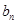 }的通项公式;
}的通项公式;
(Ⅱ)求数列{
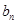 }的前
}的前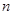 项和
项和 .
.