设f(x)= (a>0)为奇函数,且 |f(x)|min=2
(a>0)为奇函数,且 |f(x)|min=2 ,数列{an}与{bn}满足如下关系:
,数列{an}与{bn}满足如下关系:
a1=2,an+1= .
.
(1)求f(x)的解析表达式;
(2)证明:当n∈N+时,有bn≤( )n.
)n.
(本小题满分14分)已知椭圆 的两个焦点分别为
的两个焦点分别为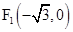 ,
,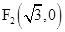 ,点
,点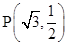 在椭圆
在椭圆
上.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)在椭圆 落在第一象限的图象上任取一点作
落在第一象限的图象上任取一点作 的切线
的切线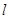 ,求
,求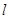 与坐标轴围成的三角形的面积的最小
与坐标轴围成的三角形的面积的最小
值;
(Ⅲ)设椭圆 的左、右顶点分别为
的左、右顶点分别为 ,
,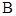 ,过椭圆
,过椭圆 上的一点
上的一点 作
作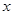 轴的垂线交
轴的垂线交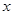 轴于点
轴于点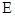 ,若
,若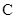 点
点
满足 ,
,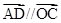 ,连结
,连结 交
交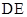 于点
于点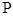 ,求证:
,求证: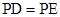 .
.
(本小题满分14分)已知数列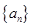 的前
的前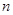 项和为
项和为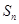 ,且
,且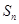 ,
, ,
, 成等差数列.
成等差数列.
(Ⅰ)求数列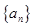 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列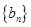 的前
的前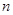 项和为
项和为 ,求证:
,求证: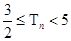 .
.
(本小题满分14分)如图,将一副三角板拼接,使他们有公共边 ,且使平面
,且使平面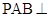 平面
平面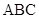 ,
,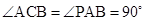 ,
,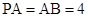 ,
,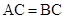 ,
,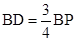 ,
,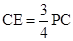 ,
, 是
是 的中点.
的中点.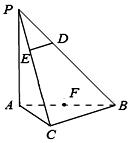
(Ⅰ)证明: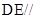 平面
平面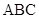 ;
;
(Ⅱ)证明: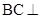 平面
平面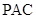 ;
;
(Ⅲ)求四棱锥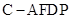 的体积.
的体积.
(本小题满分12分)从广东省某市高三第一次模拟考试成绩中,随机抽取了 名学生的数学成绩得到频率分布直方图如图所示.
名学生的数学成绩得到频率分布直方图如图所示.
(Ⅰ)根据频率分布直方图,估计该市高三学生本次模拟考试数学成绩的平均分;
(Ⅱ)若用分层抽样的方法从分数在 和
和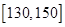 的学生中共抽取
的学生中共抽取 人,在这抽取的
人,在这抽取的 人中,随机抽取
人中,随机抽取 人,求分数在
人,求分数在 和
和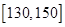 各
各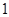 人的概率.
人的概率.
(本小题满分14分)已知函数 .
.
(1)求函数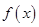 的单调区间;
的单调区间;
(2)设函数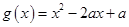 ,若对于任意
,若对于任意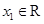 ,总存在
,总存在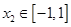 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.