等比数列
的前
项和为
,已知对任意的
,点
,均在函数
且
均为常数)的图像上.
(1)求
的值;
(11)当
时,记
,证明:对任意的
,不等式
成立.
已知函数 ,常数
,常数
(1)讨论函数 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若函数 在
在 上为增函数,求
上为增函数,求 的取值范围.
的取值范围.
数列 满足
满足 ,其中
,其中 ,求
,求 值,猜想
值,猜想 ,并用数学归纳法加以证明。
,并用数学归纳法加以证明。
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC, 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC= AB=1,M是PB的中点。
AB=1,M是PB的中点。
(1)求直线AC与PB所成角的余弦值;
(2)求面AMC与面PMC所成锐二面角的大小的余弦值。
(本小题15分)在坐标平面内有一点列 ,其中
,其中 ,
,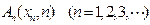 ,并且线段
,并且线段 所在直线的斜率为
所在直线的斜率为 .
.
(1)求
(2)求出数列 的通项公式
的通项公式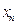
(3)设数列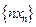 的前
的前 项和为
项和为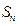 ,求
,求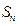 .
.
(本小题15分)若关于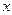 的不等式
的不等式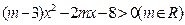 的解集是一个开区间
的解集是一个开区间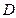 ,定义开区间
,定义开区间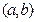 的长度
的长度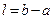 。
。
(1)求开区间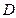 的长度
的长度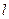 (
( 用
用 表示),并写出其定义域;
表示),并写出其定义域;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.