(本小题满分12分)数列 中,
中,
(1)求 的通项公式; (2)设
的通项公式; (2)设 ,求
,求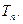
已知集合P= 的定义域为Q.
的定义域为Q.
(1)若P∩Q≠ 范围;
范围;
(2)若方程 求实数
求实数 的取值范围.
的取值范围.
某公司准备推出一个新产品,打算拨出款项3万6
千元在本地的电视台做广告,.当地电视台广告部安排该公司的广告在晚上八点前和九点后
做广告。晚八点前的广告每秒400元,九点后的广告每秒600元,每次播出的时间在10到
60秒之间。
根据市场调查研究表明,受广告影响的人数依赖于广告播出的时间以及年龄层次,受广告影响的人数总是和广告播出的时间成正比例。广告时每秒影响各年龄组的人数(千人)估计如表所示。
现在的要求是广告宣传至少要影响1 500 000个年轻人,2 000 000个中年人和2 000 000个老年人。该公司也估计了在第一个月内受广告影响的人中,每10个年轻人中有1人、20个中年人中1人、50个老年人中1人将购买一件新产品〈并且假设没有一个人第二次再买〉,则若使第一个月的销售额最大,如何来安排广告?
(文)解关于x的不等式ax2-(a+1)x+1<0。
(理)设函数 ,其中
,其中 。
。
(Ⅰ)当 时,求不等式
时,求不等式 的解集;
的解集;
(Ⅱ)若不等式 的解集为
的解集为 ,求a的值。
,求a的值。
叙述并证明余弦定理.