某公园举办雕塑展览吸引着四方宾客.旅游人数 与人均消费
与人均消费 (元)的关系如下:
(元)的关系如下: 
(1)若游客客源充足,那么当天接待游客多少人时,公园的旅游收入最多?
(2)若公园每天运营成本为 万元(不含工作人员的工资),还要上缴占旅游收入20%的税收,其余自负盈亏.目前公园的工作人员维持在40人.要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?
万元(不含工作人员的工资),还要上缴占旅游收入20%的税收,其余自负盈亏.目前公园的工作人员维持在40人.要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?
(注:旅游收入=旅游人数×人均消费)
已知函数 ,
, .
.
(Ⅰ)求证: ;
;
(Ⅱ)当0≤x≤1时,若f(x) ≥ g(x)恒成立,求a的取值范围.
已知抛物线y2 =" 2px" (p > 0)的交点为F,过 引直线l交此抛物线于A,B两点.
引直线l交此抛物线于A,B两点.
(Ⅰ)若直线AF的斜率为2,求直线BF的斜率;
(Ⅱ)若p=2,点M在抛物线上,且 ,求t的取值范围.
,求t的取值范围.
某公司招聘员工,先由两位专家面试,若两位专家都同意通过,则视作通过初审予以录用;若两位专家都未同意通过,则视作未通过初审不予录用;当这两位专家意见不一致时,再由第三位专家进行复审,若能通过复审则予以录用,否则不予录用.设应聘人员获得每位初审专家通过的概率为0.5,复审能通过的概率为0.3,各专家评审的结果相互独立.
(Ⅰ)求某应聘人员被录用的概率;
(Ⅱ)若4人应聘,设X为被录用的人数,试求随机变量X的分布列和数学期望.
已知正三棱柱ABC –A1B1C1中,AB = 2,AA1 =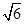 ,点F,E分别是边A1C1和侧棱BB1的中点.
,点F,E分别是边A1C1和侧棱BB1的中点.
(Ⅰ)证明:FB⊥平面AEC;
(Ⅱ)求二面角F-AE-C的余弦值.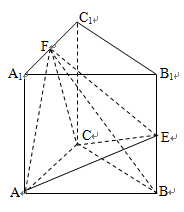
已知等比数列{an}的前n项和为Sn,A1="3," 且3S1 , 2S2 , S3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log3an,求Tn=b1b2 - b2b3 + b3b4 - b4b5 + … + b2n-1b2n - b2nb2n+1