设函数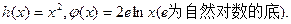
（1）求函数
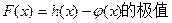； （2）若存在常数k和b,使得函数
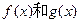对其定义域内的任意实数
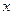分别满足
则称直线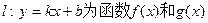
的“隔离直线”．试问:函数
是否存在“隔离直线”?若存在,求出“隔离直线”方程,不存在,请说明理由．
已知|a|＝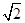
，|b|＝3，a与b夹角为45°，求使a＋λb与λa＋b的夹角为钝角时，λ的取值范围．
已知A(1,3)、B(－2，0)、C(2,1)为三角形的三个顶点，L、M、N分别是线段BC、CA、AB上的点，满足|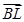
||
|＝|
||
|＝|
||
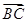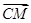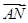|＝13，求L、M、N三点的坐标．
已知O(0,0)、A(2，－1)、B(1,3)、
＝
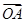＋t
，求
(1)t为何值时，点P在x轴上？点P在y轴上？点P在第四象限？
(2)四点O、A、B、P能否成为平行四边形的四个顶点，说明你的理由．
平面内给定三个向量a＝(3,2)，b＝(－1,2)，c＝(4,1)，回答下列问题：
(1)求3a＋b－2c；
(2)求满足a＝mb＋nc的实数m，n；
(3)若(a＋kc)∥(2b－a)，求实数k.
已知四点A(x,0)、B(2x,1)、C(2，x)、D(6,2x)．
(1)求实数x，使两向量
、
共线．
(2)当两向量与共线时，A、B、C、D四点是否在同一条直线上？