若动圆P恒过定点B（2，0），且和定圆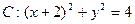
外切.
（1）求动圆圆心P的轨迹E的方程；
（2）若过点B的直线l与曲线E交于M、N两点，试判断以MN为直径的圆与直线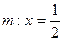
是否相交，若相交，求出所截得劣弧的弧度数，若不相交，请说明理由.
已知函数
（I）函数
在区间
上是增函数还是减函数？证明你的结论；
（II）当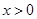
时，
恒成立，求整数
的最大值；
（Ⅲ）试证明：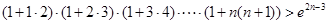
设椭圆E: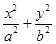
=1（
）过点M（2，
）, N（
，1），
为坐标原点
（I）求椭圆E的方程；
（II）是否存在以原点为圆心的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A，B，且
？若存在，写出该圆的方程；若不存在，说明理由。
已知点P(0,5)及圆C：x2＋y2＋4x－12y＋24＝0
（I）若直线l过点P且被圆C截得的线段长为4
，求l的方程；
（II）求过P点的圆C的弦的中点D的轨迹方程
在三棱柱ABC－A1B1C1中，AB＝BC＝CA＝AA1＝2，侧棱AA1⊥面ABC，D、E分别是棱A1B1、AA1的中点，点F在棱AB上，且
（I）求证：EF∥平面BDC1；
（II）求二面角E－BC1－D的余弦值
已知函数
，
（I）若
，求函数
的最大值和最小值，并写出相应的x的值；
（II）设
的内角
、
、
的对边分别为
、
、
，满足
，
且
，求、的值