如图，某隧道设计为双向四车道，车道总宽22m，要求通行车辆限高4.5m，隧道全长2.5km，隧道的拱线近似地看成半个椭圆形状。
（1）若最大拱高h为6m，则拱宽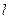
应设计为多少？
（2）若最大拱高h不小于6m，则应如何设计拱高h和拱宽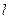，才能使建造这个隧道的土方工程量最小（半椭圆面积公式为
h）？
已知△ABC的两个顶点A(-10，2)，B(6，4)，垂心是H(5，2)，求顶点C的坐标．
已知函数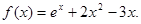
（I）求曲线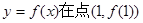
处的切线方程；
（II）当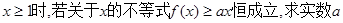
的取值范围．
如图，已知椭圆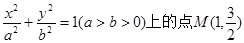
到它的两焦点F1、F2的距离之和为4，A、B分别是它的左顶点和上顶点..
（I）求此椭圆的方程及离心率；
（II）平行于AB的直线l与椭圆相交于P、Q两点，求|PQ|的最大值及此时直线l的方程.
甲乙两车间生产同一种产品，各生产40个后，按产品合格与不合格进行统计，甲车间生产的产品合格数为36个，乙车间生产的产品合格数为24个．
（1）根据以上数据完成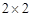
列联表；
| 不合格 |
合格 |
总计 |
|
| 甲车间 |
 |
 |
|
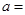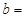| 乙车间 |
 |
 |
|
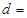| 总计 |
 |
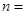（2）试判断是否产品合格与生产车间是否有关？
已知命题p：方程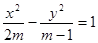
表示焦点在y轴上的椭圆；命题q：双曲线
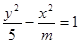的离心率
，若p、q有且只有一个为真，求m的取值范围