如图,在直三棱柱ABC-A1B1C1中, E是BC的中点。
E是BC的中点。
(1)求异面直线AE与A1C所成的角;
(2)若G为C1C上一点,且EG⊥A1C,试确定点G的位置;
(3)在(2)的条件下,求二面角A1-AG-E的大小(文科求其正切值)。
本题满分15分)已知函数 ,
, .
.
(Ⅰ)当 时,求函数
时,求函数 的极值点;
的极值点;
(Ⅱ)若函数 在导函数
在导函数 的单调区间上也是单调的,求
的单调区间上也是单调的,求 的取值范围;
的取值范围;
(Ⅲ) 当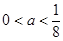 时,设
时,设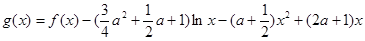 ,且
,且 是函数
是函数 的极值点,证明:
的极值点,证明: .
.
. 已知点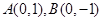 ,
,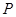 为一个动点,且直线
为一个动点,且直线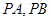 的斜率之积为
的斜率之积为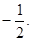
(I)求动点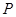 的轨迹
的轨迹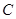 的方程;
的方程;
(II)设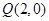 ,过点
,过点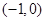 的直线
的直线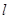 交
交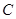 于
于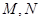 两点,
两点,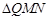 的面积记为S,若对满足条件的任意直线
的面积记为S,若对满足条件的任意直线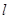 ,不等式
,不等式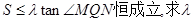 的最小值。
的最小值。
已知四边形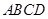 满足
满足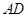 ∥
∥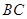 ,
,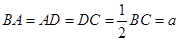 ,
,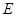 是
是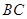 的中点,将
的中点,将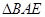 沿着
沿着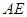 翻折成
翻折成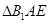 ,使面
,使面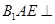 面
面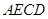 ,
,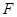 为
为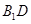 的中点.
的中点. 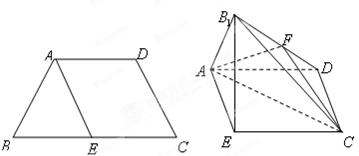
(Ⅰ)求四棱锥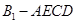 的体积;(Ⅱ)证明:
的体积;(Ⅱ)证明: ∥面
∥面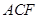 ;
;
(Ⅲ)求面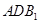 与面
与面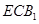 所成二面角的余弦值.
所成二面角的余弦值.
一个袋中装有大小和质地都相同的10个球,其中黑球4个,白球5个,红球1个。
(1)从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的概率分布和数学期望E(X);
(2)每次从袋中随机地摸出一球,记下颜色后放回.求3次摸球后,摸到黑球的次数大于摸到白球的次数的概率。
在 中,
中,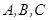 的对边分别为
的对边分别为 且
且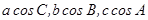 成等差数列.(1)求
成等差数列.(1)求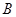 的值;(2)求
的值;(2)求 的取值范围。
的取值范围。