购买某种保险，每个投保人每年度向保险公司交纳保费
元，若投保人在购买保险的一年度内出险，则可以获得10000元的赔偿金．假定在一年度内有10000人购买了这种保险，且各投保人是否出险相互独立．已知保险公司在一年度内至少支付赔偿金10000元的概率为
.
（Ⅰ）求一投保人在一年度内出险的概率
.
（Ⅱ）设保险公司开办该项险种业务除赔偿金外的成本为50000元，为保证盈利的期望不小于0，求每位投保人应交纳的最低保费（单位：元）.
已知二次函数f(x)=px2+qx(p≠0),其导函数为f'(x)=6x-2,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(1)求数列{an}的通项公式.
(2)若cn=
(an+2),2b1+22b2+23b3+…+2nbn=cn,求数列{bn}的通项公式.
若虚数z同时满足下列两个条件:
①z+
是实数;②z+3的实部与虚部互为相反数.
这样的虚数是否存在?若存在,求出z;若不存在,请说明理由.
已知关于x的方程:x2-(6+i)x+9+ai=0(a∈R)有实数根b.
(1)求实数a,b的值.
(2)若复数满足|
-a-bi|-2|z|=0,求z为何值时,|z|有最小值,并求出|z|的最小值.
已知M(1+cos 2x,1),N(1,
sin2x+a)(x∈R,a∈R,a是常数),且y=
·
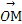(O为坐标原点).
(1)求y关于x的函数关系式y=f(x).
(2)若x∈[0,
]时,f(x)的最大值为2013,求a的值.
已知A,B,C三点的坐标分别为A(3,0),B(0,3),C(cosα,sinα),其中α∈(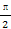
,
).
(1)若|
|=|
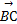|,求角α的值.
(2)若·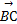=-1,求tan(α+
)的值.